Triángulo rectángulo: características y fórmulas

Como seguro sabes bien, existen diferentes tipos de triángulos, según sus características: hoy vamos a hablar del triángulo rectángulo, después de habernos ocupado ya del isósceles y el equilátero.

Vamos a ver cuáles son sus características, sus propiedades, y las principales fórmulas para calcular altura, área y perímetro de un triángulo rectángulo.

Características del triángulo rectángulo

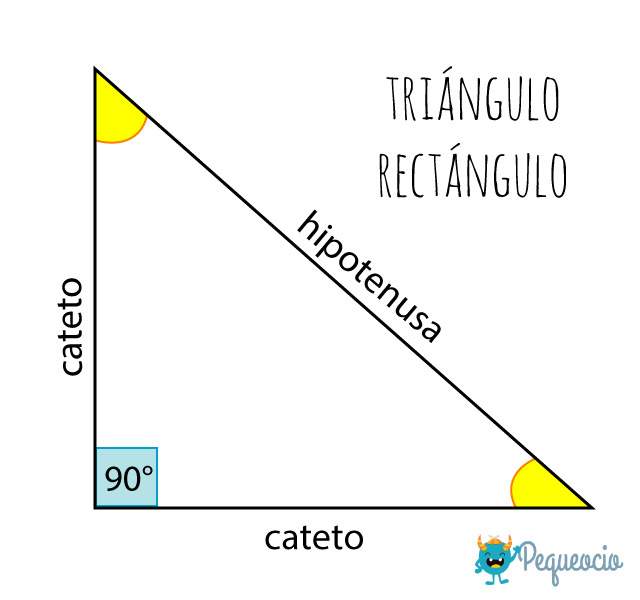
Un triángulo rectángulo es un tipo de triángulo con un ángulo recto, es decir un ángulo de 90°

En los triángulos rectángulos se cumple el famoso Teorema de Pitágoras:

En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Este teorema nos va a servir luego, por lo que hablaremos más sobre él.

Los elementos de un triángulo rectángulo son: los dos lados contiguos al ángulo recto, a y b (cada uno de ellos es un cateto), y el lado mayor c, opuesto al ángulo recto, que es la hipotenusa.

Tipos de triángulos rectángulos

Existen dos tipos:

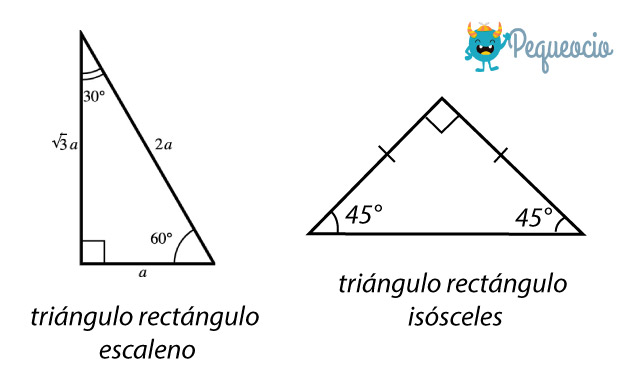
• Triángulo rectángulo isósceles: los dos catetos (los lados que forman el ángulo recto) son de la misma longitud, los ángulos interiores son de 45-45-90. En este tipo de triángulo, la hipotenusa mide √2 veces la longitud del cateto.
• Triángulo rectángulo escaleno: los tres lados y los tres ángulos tienen diferente medida. Un caso particular es aquél cuyos ángulos interiores miden 30-60-90, en este tipo de triángulo, la hipotenusa (el lado opuesto al ángulo recto) mide el doble del cateto menor, y el cateto mayor √3 veces la longitud del cateto menor.

APRENDE SOBRE EL TRIÁNGULO ISÓSCELES

APRENDE SOBRE EL TRIÁNGULO EQUILÁTERO

Propiedades del triángulo rectángulo

Todos los triángulos rectángulos tienen propiedades en común. Pero antes de hablar de ellas tenemos  que aclarar el significado de algunos términos:

• Mediana: es una recta que parte desde el punto medio de un lado, y llega al vértice opuesto. Las tres medianas concurren en un punto llamado baricentro.
• Altura: es la recta que va desde el vértice hasta el lado que es opuesto y además esta recta es perpendicular a dicho lado. Las tres alturas concurren en un punto llamado ortocentro.

Ahora que tenemos claro el significado de algunos términos, veamos algunas de las propiedades o proposiciones de los triángulos rectángulos:

• Tiene dos ángulos agudos.
• La hipotenusa es mayor que cualquiera de los catetos.
• La longitud del cuadrado de la hipotenusa es igual a la suma de la longitud de los cuadrado de los catetos (teorema de Pitágoras)
• La suma de la longitud de la hipotenusa y el diámetro de un círculo inscrito en el triángulo es igual a la suma de la longitud de los catetos.
• La mediana de la hipotenusa descompone un triángulo rectángulo escaleno en dos triángulos: uno obtusángulo y otro acutángulo, no congruentes pero equivalentes.
• La mediana de la hipotenusa de un triángulo rectángulo isósceles lo descompone en dos triángulos rectángulos isósceles congruentes y equivalentes.
• La mediana que parte del ángulo recto es igual a la mitad de la hipotenusa.
• La altura que parte del vértice del ángulo recto, coincide con un cateto, con tal de considerar al otro cateto como una base.

Las fórmulas

Vamos a ver ahora cómo se calculan la altura, el área y el perímetro de los T.R.:

Cómo calcular la altura de un triángulo rectángulo

Hemos dicho ya (si bien con otras palabras) que si se considera a uno de los catetos como la base del triángulo, el otro cateto será siempre la altura (h). Dicho de otro modo:

Las alturas asociadas a los catetos (a y b) son el cateto opuesto correspondiente.

Por lo tanto:

 

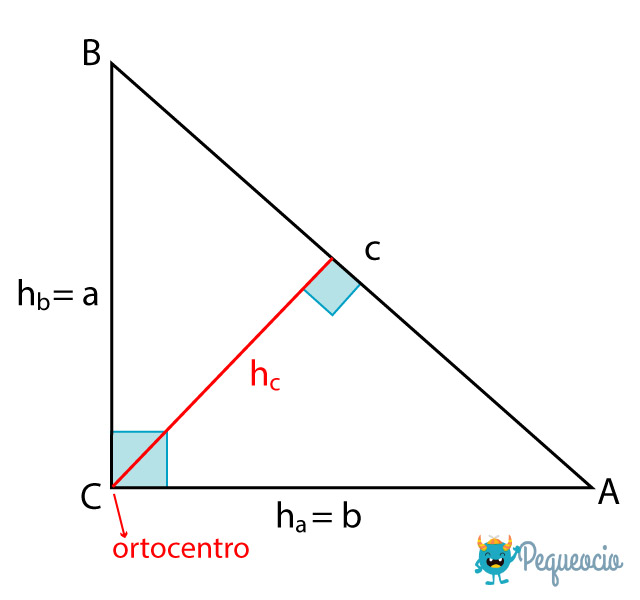
h_a= b (la altura asociada al cateto a es igual al cateto b)

h_b= a (la altura asociada al cateto b es igual al cateto a)

La altura asociada a la hipotenusa es h_c

Las tres alturas confluyen en el ortocentro, que es el vértice C del ángulo recto.

Si conocemos las longitudes de la base y la hipotenusa, podemos calcular la altura (h) usando el teorema de Pitágoras.

El teorema de Pitágoras

Este teorema relaciona los catetos de un triángulo rectángulo con su hipotenusa. Un triángulo rectángulo tiene un ángulo recto de 90° y dos ángulos menores (< 90°). Los dos lados que forman el ángulo recto son los catetos. El lado mayor opuesto al ángulo recto es la hipotenusa. El teorema de Pitágoras enuncia que:

Todos los triángulos rectángulos cumplen que la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado. 

Es decir:

c² = a² + b²

Siendo a y b los dos catetos, y c la hipotenusa.

Tendremos que despejar el dato que nos falta para obtener el resultado.

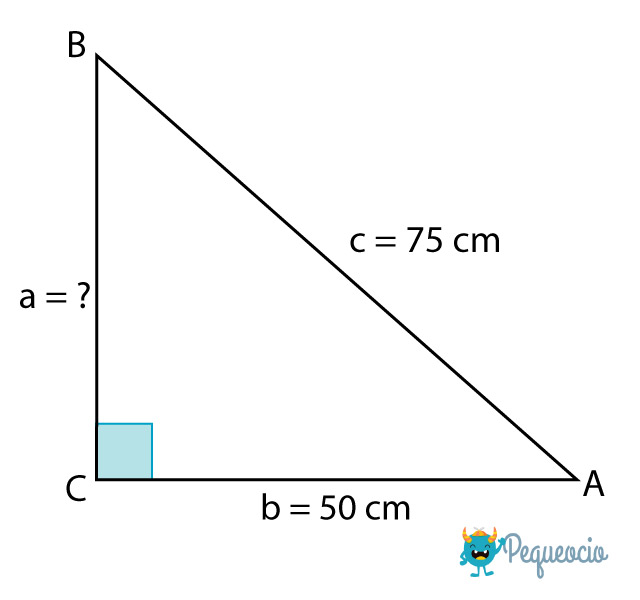
La altura de nuestro triángulo es el cateto a. Por lo tanto vamos a despejar a:

c² = a² + b²

c² – b² = a²  que es lo mismo que decir  a² = c² – b²

Ya podemos reemplazar con los datos que tenemos

a² = (75 cm)² – (50 cm)²

a² = 5.625 cm² – 2.500 cm²

a² = 3.125 cm²

Quitamos el cuadrado aplicando raíz cuadrada:

√a² = √3.125 cm²

a = 55,9 cm

La altura de nuestro triángulo, es decir la longitud del cateto a, es 55,9 cm.

Calcular la altura relativa a la hipotenusa

Hasta ahora hemos visto cómo calcular la altura de un triángulo que tiene un cateto como base, pero ¿cómo calculamos la altura de un triángulo con la hipotenusa como base? Necesitamos conocer las longitudes de los dos catetos y de la hipotenusa.

 

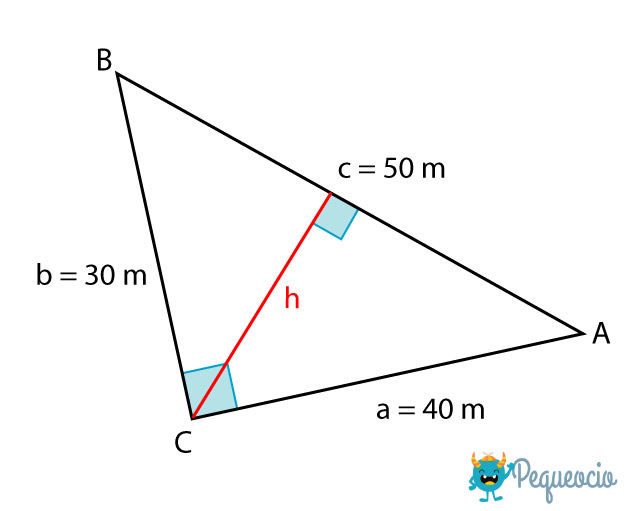
Para calcular la altura relativa a la hipotenusa vamos a calcular primero el área del triángulo. Recordemos que no importa qué lado tomemos como base, el área del triángulo será siempre igual. Por lo tanto vamos a calcular el área tomando como base a, y por lo tanto la altura será b.

El área de un triángulo  se calcula multiplicando la base (b) por la altura(h) y dividiendo entre 2:

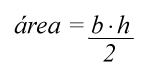
Reemplazamos con los datos que tenemos:

A = (40m).(30m) / 2

A = 1.200 m² /2

A = 600 m²

El área de este triángulo es 600 m². Y como hemos dicho, no cambia si tomamos otro de los lados como base. Queremos calcular la altura de este triángulo tomando la hipotenusa como base, así que usaremos siempre la fórmula para calcular el área, reemplazando los datos que tenemos: el área (600 m²), y la base (50 m)

Primero  vamos a simplificar la fórmula multiplicando todo por 2, con el objetivo de cancelar el 2 que divide:

2(A) = (b.h /2)2

Nos queda que:

2A = b.h

Despejamos la altura (h) pasando la base del otro lado dividiendo:

2A/b = h

Reemplazamos con los datos que conocemos:

2(600 m²) /50 m = h

1.200 m² / 50 m = h 

Dividimos 1.200 por 50 y nos da 24. El cuadrado de 1.200 m² se cancela con el m de 50, por lo que en el resultado nos queda solo m:

24 m = h

Ya tenemos el resultado, la altura del triángulo relativa a la hipotenusa es 24 m

Cómo calcular el área de un triángulo rectángulo

El área de un triángulo rectángulo se calcula multiplicando la base (a) por la altura (h) y dividiendo entre 2:

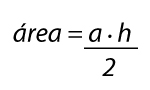
Cómo calcular el perímetro de un triángulo rectángulo

El perímetro de un triángulo es la suma de sus tres lados.

Perímetro = a + b + c

Como en los triángulos rectángulos se cumple el teorema de Pitágoras y podemos saber cuánto mide la hipotenusa (c) partiendo de los catetos (a y b), en el caso de que no conozcamos la medida de la hipotenusa la fórmula sería así:

Existen otros modos de calcular altura, perímetro y área de un triángulo, pero son más complejas y requieren de conocimientos matemáticos más avanzados. Por ahora, y como nos ocupamos de recursos didácticos para niños de primaria, nos quedaremos con las que hemos visto anteriormente.

Sabemos que puede parecer todo complicado en un principio, pero es solo cuestión de práctica, ¡anímate!