Seguro que ya sabes que existen diferentes tipos de triángulos: triángulo isósceles, triángulo equilátero, escaleno, pero… ¿sabrías definir las características de cada uno? Hoy nos vamos a ocupar del triángulo isósceles: de sus características, de las fórmulas necesarias para calcular la altura, el área, el perímetro y la base.
¿Estás listo para comenzar este viaje geométrico? ¡Vamos a ello!
ÍNDICE DE CONTENIDOS
Características del triángulo isósceles
Un triángulo isósceles es un tipo de triángulo que tiene dos lados de igual longitud
Los dos lados iguales se llaman patas -el término isósceles proviene de la unión de dos palabras griegas: “isos” (igual) y “skelos” (pierna)- y el lado desigual se llama base.
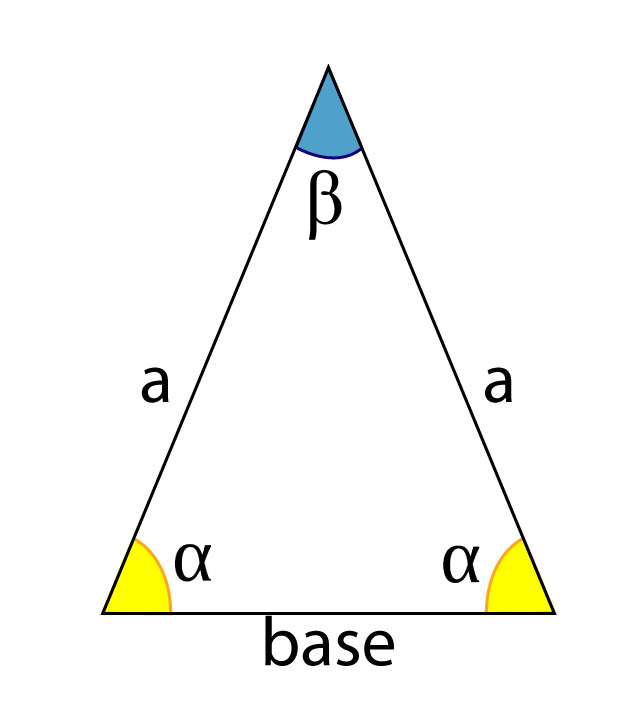
Una característica de los triángulos isósceles es que los ángulos internos (?) opuestos a los lados iguales (a) son de la misma medida, mientras que el tercer ángulo (?),llamado ángulo en el vértice, es diferente, y formado por los dos lados de igual longitud:
Según la amplitud de los ángulos internos, los triángulos isósceles pueden ser:
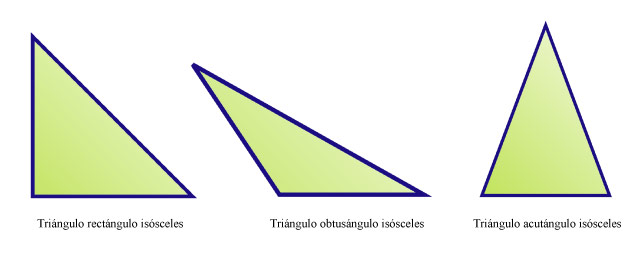
- Triángulo rectángulo isósceles: uno de sus ángulos es recto (90°), y los otros dos son iguales (45°)
- Triángulo obtusángulo isósceles: uno de sus lados es obtuso (>90°)
- Triángulo acutángulo isósceles: todos sus ángulos son agudos (< 90°), y dos tienen la misma medida
Propiedades del triángulo isósceles
Todos los triángulos isósceles tienen propiedades o proposiciones en común. Pero antes de hablar de ellas tenemos que aclarar el significado de algunos términos:
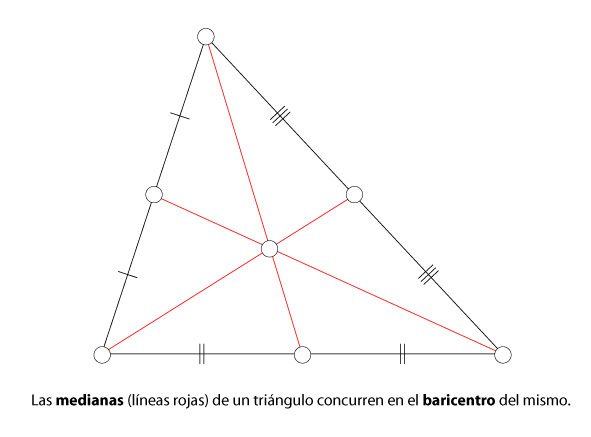
- Mediana: es una recta que parte desde el punto medio de un lado, y llega al vértice opuesto. Las tres medianas concurren en un punto llamado baricentro.
- Bisectriz: La bisectriz de un ángulo es la semirrecta con origen en el vértice del ángulo y que lo divide en dos ángulos de igual medida.
- Mediatriz: La mediatriz de un segmento es la línea recta perpendicular a dicho segmento trazada por su punto medio.
- Altura: es la recta que va desde el vértice hasta el lado que es opuesto y además esta recta es perpendicular a dicho lado.
Ahora que tenemos claro el significado de algunos términos, veamos algunas de las propiedades o proposiciones de los triángulos isósceles:
- Los ángulos internos opuestos a los lados iguales son de la misma medida, mientras que el tercer ángulo (llamado ángulo en el vértice) es diferente, y formado por los dos lados de igual longitud.
- Cualquier triángulo con dos bisectrices de igual longitud es isósceles. Esta proposición es conocida como el teorema de Steiner-Lehmus.
- En un triángulo isósceles la mediatriz de su base es eje de simetría, porque es también bisectriz.
- La recta que es trazada desde el vértice opuesto a la base hasta el punto medio de la base del triángulo isósceles, es a la vez la altura, la mediana y la mediatriz, así como también la bisectriz relativa al ángulo opuesto de la base.
- Los dos ángulos opuestos a los lados iguales son siempre agudos, es decir que miden siempre menos de 90°.
- Cualquier segmento paralelo a la base de un triángulo isósceles, con extremos en los lados iguales, determina un triángulo semejante al triángulo original.
- En un triángulo isósceles, la mediatriz de la base determina dos triángulos rectángulos iguales (congruentes)
Las fórmulas
Vamos a ver ahora cómo se calculan la altura, el área, el perímetro y la base de los triángulos isósceles:
Cómo calcular la altura del triángulo isósceles
Para calcular la altura (h) de un isósceles usaremos el teorema de Pitágoras.
¿Qué es el teorema de Pitágoras?
Este teorema relaciona los catetos de un triángulo rectángulo con su hipotenusa. Un triángulo rectángulo tiene un ángulo recto de 90° y dos ángulos menores (< 90°). Los dos lados que forman el ángulo recto son los catetos. El lado mayor opuesto al ángulo recto es la hipotenusa. El teorema de Pitágoras enuncia que:
Todos los triángulos rectángulos cumplen que la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado.
Es decir:
c² = a² + b²
Siendo a y b los dos catetos, y c la hipotenusa.
Bien, entonces ¿cómo usamos el teorema de Pitágoras para calcular la altura de un triángulo isósceles? Hemos dicho antes que la altura (h) de la base determina dos triángulos rectángulos iguales. Entonces, en un isósceles, los lados a, b/2 (la mitad de la base) y h forman un triángulo rectángulo. Y por lo tanto los lados b/2 y h son los catetos, y a es la hipotenusa de dicho triángulo, podemos entenderlo mejor en la imagen:
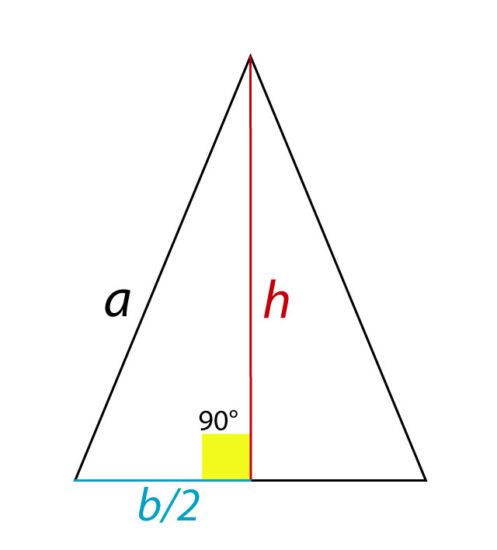
Entonces utilizando el teorema de Pitágoras, podemos determinar el valor de la altura:
a² (cateto) + b² (cateto) = c² (hipotenusa)
En nuestro triángulo:
a² = altura (h)
b² = b/2
c² = a
Debemos sustituir los valores del teorema con los nuestros, y despejar la altura:
h² + (b/2)² = a²
h² + b²/4 = a²
h² = a² – b²/4
h = √ (a² – b²/4)
Hemos obtenido que la altura es:
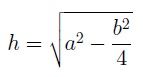
Cómo calcular el área del triángulo isósceles
El área de un triángulo isósceles se calcula multiplicando la base (b) por la altura (h) y dividiendo entre 2:
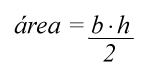
Ya sabemos la fórmula para calcular la altura, la sustituímos en la fórmula del área y nos queda así:
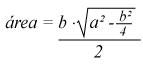
TAMBIÉN TE PUEDE INTERESAR: Cómo calcular el área del círculo
Cómo calcular el perímetro del triángulo isósceles
Ahora vamos a ver cómo se calcula el perímetro (p) del triángulo. Pues es muy sencillo, porque se calcula sumando los lados. Como en este caso el triángulo isósceles tiene dos lados de la misma medida, podemos expresar la fórmula del siguiente modo:
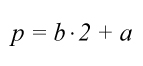
Cómo calcular la base del triángulo isósceles
Nos queda aprender cómo calcular la base del triángulo. Como los triángulos isósceles tienen dos lados iguales, para calcular la base necesitamos conocer la altura:
Si conocemos la altura, usamos de nuevo el teorema de Pitágoras:
a² + b² = c²
donde:
a² = altura (h)
c² = el lado a
b² = b/2 (el dato que no conocemos)
Por lo tanto tenemos que despejar b²:
b² = c² – a²
b = √ c² – a²
Recordemos que el valor que hemos obtenido corresponde a la mitad de la base (b/2), por lo que tenemos que multiplicar por 2 para obtener la medida de la base del triángulo:
b = 2 * (√ c² – a²)
Existen otros modos de calcular altura, perímetro, área y base de un triángulo, pero son más complejas y requieren de conocimientos matemáticos más avanzados. Por ahora, y como nos ocupamos de recursos didácticos para niños de primaria, nos quedaremos con las que hemos visto anteriormente.
¿Te ha quedado claro qué es un triángulo isósceles?
PIN IT>> Sigue nuestros tableros en Pinterest