Triángulo equilátero: características y fórmulas

Como sabes, existen diferentes tipos de triángulos: triángulo equilátero, triángulo isósceles, escaleno, pero… ¿sabrías definir las características de cada uno y en qué se diferencian? Hace unos días vimos el isósceles, hoy nos vamos a ocupar del equilátero: de sus características, de las fórmulas necesarias para calcular la altura, el área, y el perímetro.

¿Estás listo para aprender un poquito más de geometría? ¡Vamos a ello!

Características del triángulo equilátero

Un triángulo equilátero es un tipo de triángulo que tiene los tres lados iguales.

Un triángulo equilátero es un polígono regular, es decir que sus tres lados (a) tienen la misma longitud. Además, los triángulos equiláteros son equiangulares, es decir que los tres ángulos internos son iguales, y miden 60°.

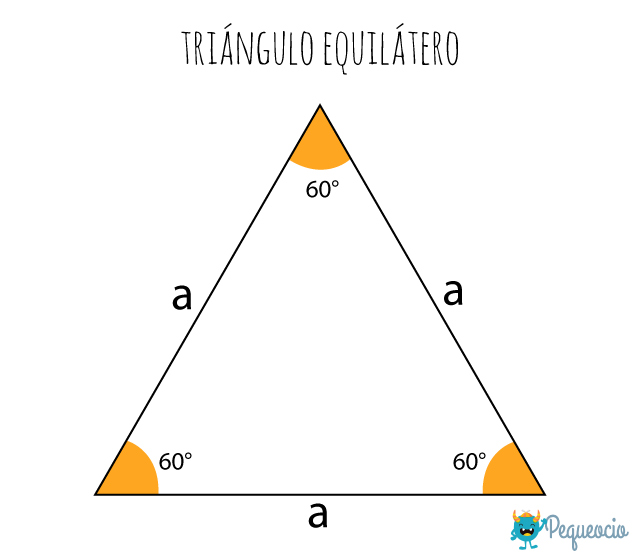
 Propiedades del triángulo equilátero

Los triángulos equiláteros tienen tres ejes de simetría: cada uno de ellos pasa por un vértice y el punto medio del lado opuesto. Pero antes de hablar de las propiedades del triángulo equilátero tenemos  que aclarar el significado de algunos términos:

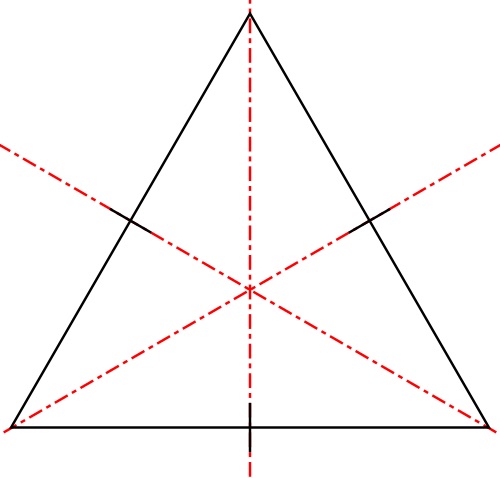
• Mediana: es una recta que parte desde el punto medio de un lado, y llega al vértice opuesto. Las tres medianas concurren en un punto llamado baricentro.
• Bisectriz: La bisectriz de un ángulo es la semirrecta con origen en el vértice del ángulo y que lo divide en dos ángulos de igual medida. Las tres bisectrices concurren en un punto llamado incentro.
• Mediatriz: La mediatriz de un segmento es la línea recta perpendicular a dicho segmento trazada por su punto medio.
• Altura: es la recta que va desde el vértice hasta el lado que es opuesto y además esta recta es perpendicular a dicho lado. Las tres alturas concurren en un punto llamado ortocentro.

Ahora que tenemos claro el significado de algunos términos, veamos algunas de las propiedades o proposiciones de los triángulos equiláteros:

1. Cada altura, mediana, bisectriz, mediatriz y eje de simetría de un triángulo equilátero coinciden sobre una misma recta. Por tanto el ortocentro, el baricentro, el incentro y el circuncentro (centro de la circunferencia circunscrita a un triángulo) coinciden en un mismo punto central.
2. Dos triángulos equiláteros cualquiera son siempre semejantes.

Las fórmulas

Vamos a ver ahora cómo se calculan la altura, el área y el perímetro de los triángulos equiláteros:

Cómo calcular la altura del triángulo equilátero

Para calcular la altura (h) de un equilátero usaremos el teorema de Pitágoras.

¿Qué es el teorema de Pitágoras?

Este teorema relaciona los catetos de un triángulo rectángulo con su hipotenusa. Un triángulo rectángulo tiene un ángulo recto de 90° y dos ángulos menores (< 90°). Los dos lados que forman el ángulo recto son los catetos. El lado mayor opuesto al ángulo recto es la hipotenusa. El teorema de Pitágoras enuncia que:

Todos los triángulos rectángulos cumplen que la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado. 

Es decir:

c² = a² + b²

Siendo a y b los dos catetos, y c la hipotenusa.

Bien, entonces ¿cómo usamos el teorema de Pitágoras para calcular la altura de un triángulo equilátero? Podemos ver que en un  equilátero, los lados a, a/2 (la mitad de la base) y h (altura) forman un triángulo rectángulo. Y por lo tanto los lados a/2 y h son los catetos, y a es la hipotenusa de dicho triángulo, podemos entenderlo mejor en la imagen:

 

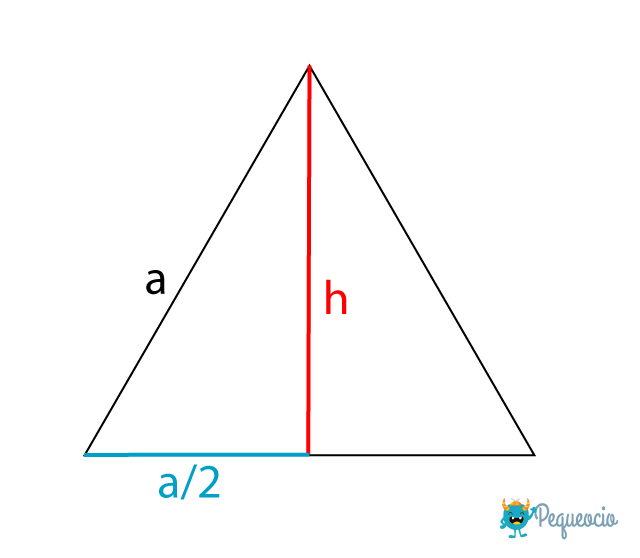
Entonces utilizando el teorema de Pitágoras, podemos determinar el valor de la altura:

 a² (cateto) + b² (cateto) = c² (hipotenusa)

En nuestro triángulo:

a² = altura (h)

b² = a/2

c² = a

Debemos sustituir los valores del teorema con los nuestros, y despejar la altura:

h² + (a/2)² = a²

h² = a² – (a/2)² 

 

 

Hemos obtenido que la altura es:

 

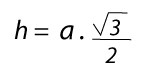
Pero lo vamos a entender mejor con un ejemplo práctico: vamos a calcular la altura de un triángulo de 10 cm de lado.

Sabemos entonces que la hipotenusa mide 10 cm, y el cateto b mide 5cm, porque es la mitad de un lado. Entonces partimos del teorema de Pitágoras, reemplazando los datos que tenemos:

 a²  + b²  = c² 

h² + 5² = 10²

Calculamos los cuadrados de los datos que conocemos:

h² + 25 = 100

Aislamos la altura:

h²  = 100 -25

h² = 75

Despejamos la altura:

h = √75 = 8,66

Por lo tanto, la altura del rectángulo es 8,66 cm. Si lo comprobáis aplicando la fórmula que vimos antes veréis que llegáis al mismo resultado.

Cómo calcular el área del triángulo equilátero

El área de un triángulo equilátero se calcula multiplicando la base (a) por la altura (h) y dividiendo entre 2:

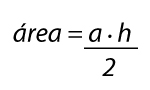
Ya sabemos la fórmula para calcular la altura, la sustituímos en la fórmula del área y nos queda así:

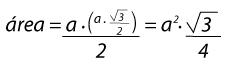
Tenemos entonces que la fórmula para calcular el área de un equilátero es:

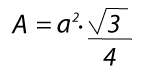
Cómo calcular el perímetro del triángulo equilátero

Ahora vamos a ver cómo se calcula el perímetro (p) del triángulo. Pues es muy sencillo, porque se calcula multiplicando la longitud de un lado por 3, ya que los tres lados de los triángulos equiláteros son iguales. Por lo tanto: p = 3 . a

Existen otros modos de calcular altura, perímetro y área de un triángulo, pero son más complejas y requieren de conocimientos matemáticos más avanzados. Por ahora, y como nos ocupamos de recursos didácticos para niños de primaria, nos quedaremos con las que hemos visto anteriormente.

¡Solo necesitas hacer un poco de práctica!

PIN IT>> Sigue nuestros tableros en Pinterest