El triángulo: tipos de triángulos y fórmulas (para primaria)

Hemos ya hablado sobre varias clases de triángulos, pero ha llegado el momento de reunir toda la información en un mismo lugar: vamos a aprender qué es y cuáles son sus propiedades; qué tipos de triángulos hay según la medida de sus lados o de sus ángulos; y cuáles son las fórmulas que se utilizan en primaria.

Como hemos aclarado, la información que encontraréis en este post está dirigida a alumnos de primaria, por lo que no nos ocuparemos de contenidos más avanzados que se ven más adelante.

¿Qué es un triángulo?

Un triángulo es un polígono de tres lados.

Recordemos que un polígono es una figura geométrica plana compuesta por una secuencia finita de segmentos rectos consecutivos (los lados) que encierran una región en el plano.

Elementos

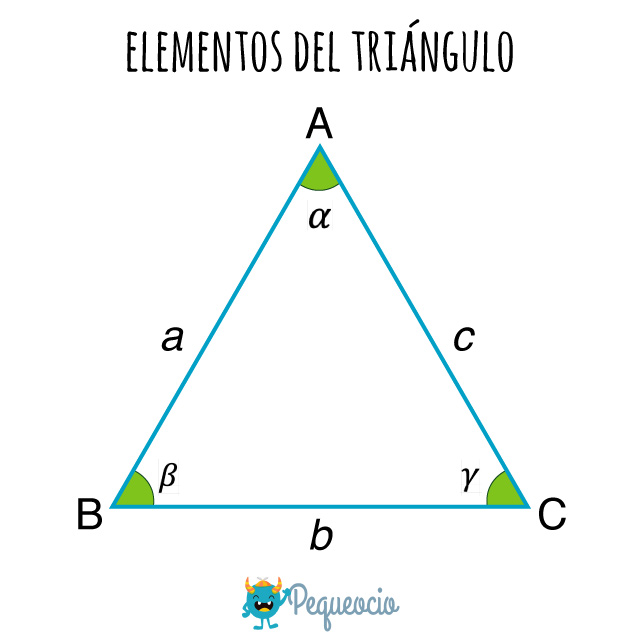
Los elementos de un triángulo son:

• Lado (a, b, c): cada uno de los segmentos que lo componen.
• Vértice (A,B,C): punto de unión entre los lados consecutivos.
• Ángulo interior (?, ?, ?): es el ángulo formado, internamente al polígono, por dos lados consecutivos.

Propiedades de los triángulos

• El triángulo es el polígono más simple y el único que no tiene diagonal.
• Tres puntos no alineados definen siempre un triángulo.
• La suma de los tres ángulos internos de un triángulo es siempre 180°
• La suma de las longitudes de dos lados de un triángulo es siempre mayor que la longitud del tercer lado.
• Los triángulos son los únicos polígonos que son siempre convexos, nunca pueden ser cóncavos dado que ninguno de sus tres lados pueden superar los 180°.

Tipos de triángulos según sus lados

Según la longitud de sus lados se clasifican en:

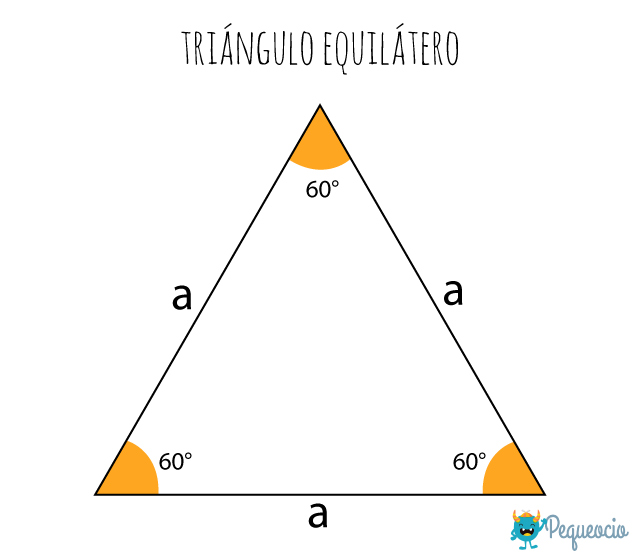
Triángulo equilátero

Un triángulo equilátero es un tipo de triángulo que tiene los tres lados iguales.

Los triángulos equiláteros son polígonos regulares (porque tienen todos sus lados de la misma longitud. Además son equiangulares, porque también sus ángulos son iguales: miden 60°.

Hemos preparado un post con toda la información sobre los equiláteros: características, propiedades y fórmulas> TRIÁNGULO EQUILÁTERO

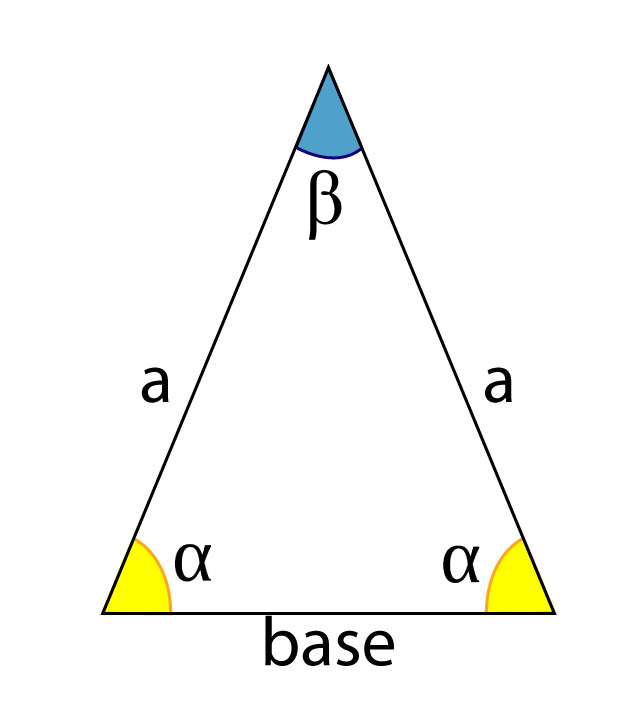
Triángulo isósceles

Un triángulo isósceles es un tipo de triángulo que tiene dos lados de igual longitud.

El término isósceles proviene de la unión de dos palabras griegas: «isos» (igual) y «skelos» (pierna o pata), porque los dos lados iguales se llaman patas, y el restante base. 

En los triángulos isósceles los ángulos internos (?) opuestos a los lados iguales (a) son de la misma medida, mientras que el tercer ángulo (?), formado por los dos lados de igual longitud es diferente, y se llama ángulo en el vértice.

Aprende más sobre las características, propiedades y las fórmulas aquí> TRIÁNGULO ISÓSCELES

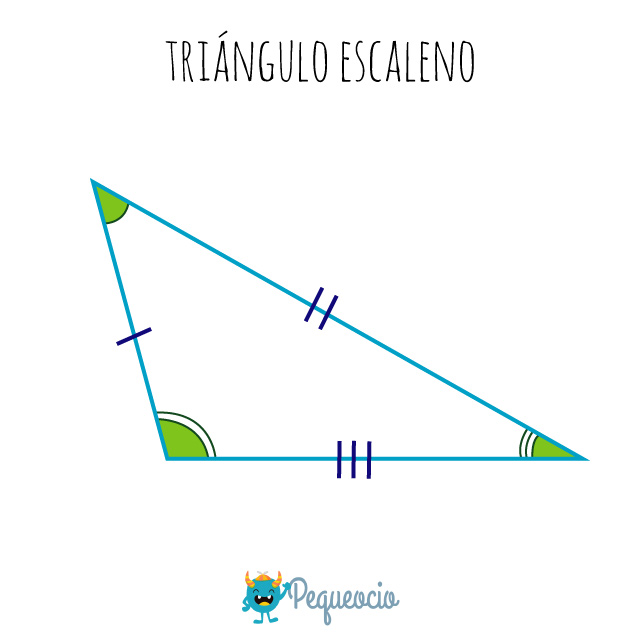
Triángulo escaleno

Un triángulo escaleno tiene todos los lados y los ángulos diferentes.

Como en todos los triángulos, la suma de sus ángulos da 180°.

Tipos de triángulos según sus ángulos

Según la amplitud de sus ángulos internos se clasifican en:

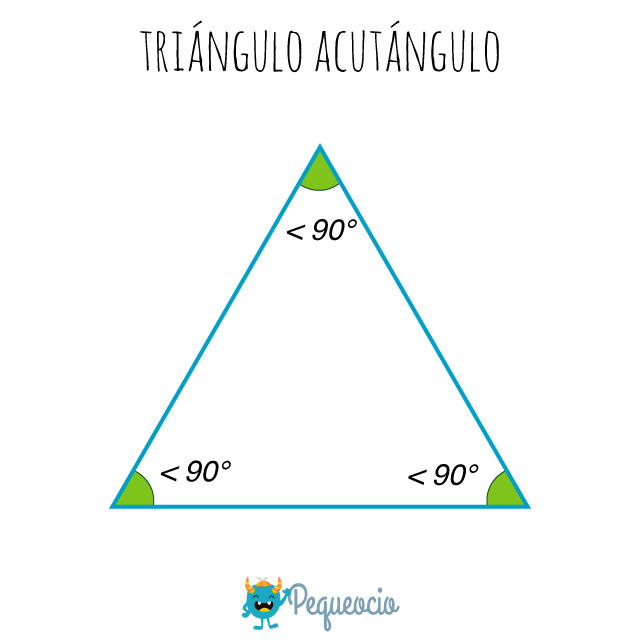
Triángulo acutángulo

El triángulo acutángulo tiene todos sus ángulos agudos (< 90°).

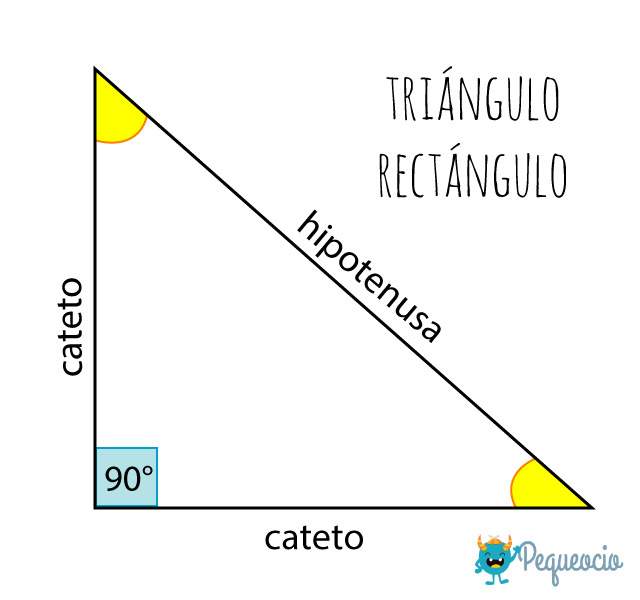
Triángulo rectángulo

Un triángulo rectángulo tiene un ángulo recto, es decir un ángulo de 90°.

En los triángulos rectángulos se cumple el famoso Teorema de Pitágoras:

En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Pero no os preocupéis que lo vamos a explicar más abajo, porque es un teorema muy importante en geometría.

Aprende más aquí> TRIÁNGULO RECTÁNGULO

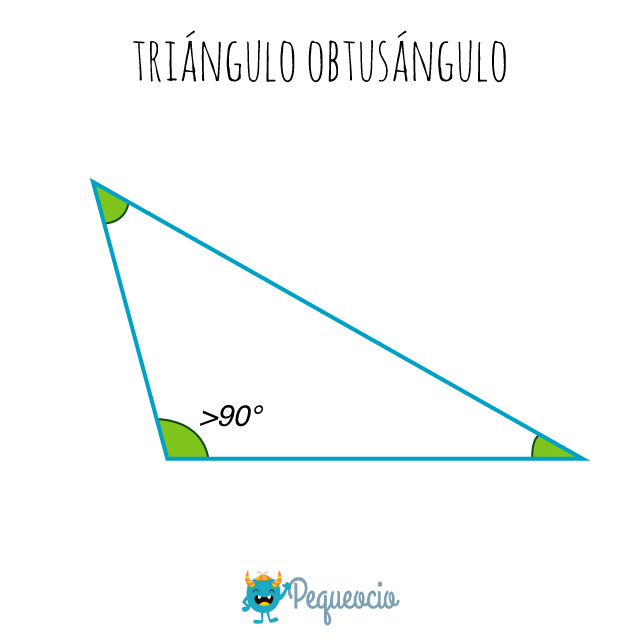
Triángulo obtusángulo

Cuando uno de sus ángulos es obtuso (>90°) y por lo tanto los otros dos agudos (<90°).

Cuando ninguno de los ángulos internos es recto, el triángulo es oblicuángulo. Por ello, los obtusángulos y acutángulos son oblicuángulos.Cualquier triángulo o bien es rectángulo o bien oblicuángulo.

Las fórmulas

Antes de ver las fórmulas para calcular el área, la altura y el perímetro de un triángulo tenemos que ver el teorema de Pitágoras, que es fundamental para poder entender algunas fórmulas.

El teorema de Pitágoras

Este teorema relaciona los catetos de un triángulo rectángulo con su hipotenusa. Un triángulo rectángulo tiene un ángulo recto de 90° y dos ángulos menores (< 90°). Los dos lados que forman el ángulo recto son los catetos. El lado mayor opuesto al ángulo recto es la hipotenusa. El teorema de Pitágoras enuncia que:

Todos los triángulos rectángulos cumplen que la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado. 

Es decir:

c² = a² + b²

Siendo a y b los dos catetos, y c la hipotenusa.

Altura del triángulo

¿Cómo usamos el teorema de Pitágoras para calcular la altura de un triángulo isósceles o un equilátero? Podemos ver que en un  equilátero o un isósceles, los lados a, a/2 (la mitad de la base) y h (altura) forman un triángulo rectángulo. Y por lo tanto los lados a/2 y h son los catetos, y a es la hipotenusa de dicho triángulo, podemos entenderlo mejor en la imagen:

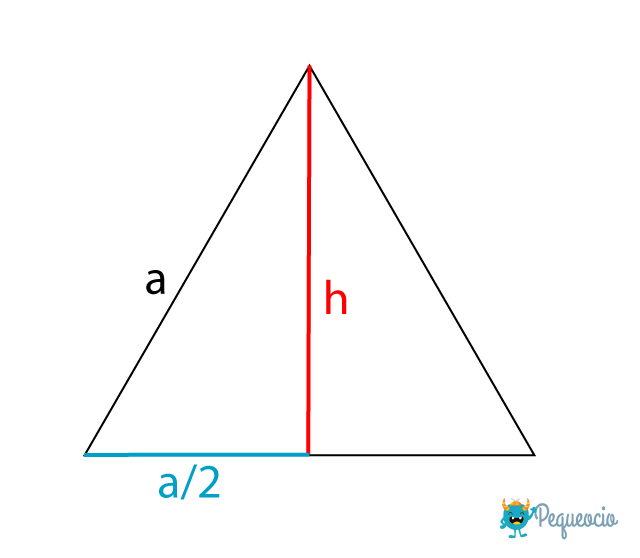
Entonces utilizando el teorema de Pitágoras, podemos determinar el valor de la altura:

 a² (cateto) + b² (cateto) = c² (hipotenusa)

En nuestro triángulo:

a² = altura (h)

b² = a/2

c² = a

Debemos sustituir los valores del teorema con los nuestros, y despejar la altura:

h² + (a/2)² = a²

h² = a² – (a/2)² 

 

 

Hemos obtenido que la altura es:

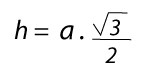
En el caso del triángulo escaleno no es posible usar el teorema de Pitágoras, porque todos los lados son diferentes. Si se conoce la medida de todos los lados se usa la fórmula de Herón, pero es un procedimiento demasiado complejo para primaria, por lo que no lo explicaremos en esta ocasión.

Área del triángulo

La fórmula general para calcular el área de un triángulo es:

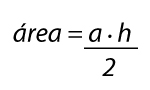
Es decir que se calcula multiplicando la base (a) por la altura (h) y dividiendo entre 2. Para poder utilizar esta fórmula necesitamos conocer la medida de uno de los lados del triángulo (que ejercerá como base) y la altura asociada a dicho lado, que es la recta que va desde la base al vértice opuesto:

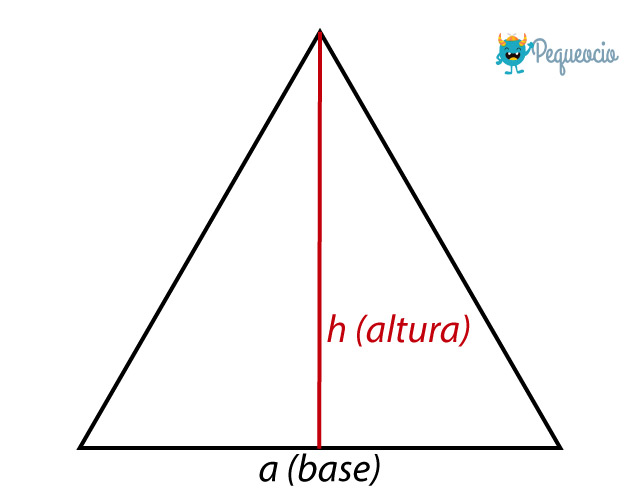
Si no conocemos la altura del triángulo podemos reemplazar el dato con la fórmula para calcular la altura. Podéis ver la explicación, con ejemplos, aquí> CÓMO CALCULAR EL ÁREA DE UN TRIÁNGULO

Perímetro del triángulo

El perímetro de un triángulo es la suma de sus lados:

P = a + b + c

En el caso de un triángulo equilátero, como todos sus lados son iguales, es suficiente multiplicar la longitud de un lado por 3:

P = 3 . a

El triángulo isósceles tiene dos lados de la misma medida, podemos expresar la fórmula del siguiente modo:

P = a.2 + b

Existen otros modos de calcular altura, perímetro y área de un triángulo, pero son más complejas y requieren de conocimientos matemáticos más avanzados. Por ahora, y como nos ocupamos de recursos didácticos para niños de primaria, nos quedaremos con las que hemos visto anteriormente.