¿Llegó el momento de aprender a hacer operaciones con fracciones? Pues en Pequeocio te vamos a ayudar con una guía completísima donde vamos a aprender paso a paso a hacer sumas, restas, multiplicaciones y divisiones con fracciones.
Antes de empezar, si tienes dudas sobre qué es una fracción, qué tipos hay, qué es una fracción equivalente y cómo comparar fracciones, lee nuestro artículo sobre FRACCIONES FÁCILES PARA PRIMARIA.
ÍNDICE DE CONTENIDOS
Operaciones con fracciones
Las operaciones con fracciones no se limitan a las sumas, restas, multiplicaciones y divisiones. Pero como no podemos abarcarlo todo en un solo artículo, y además queremos comenzar por las bases, vamos a hablar de suma y resta de fracciones, multiplicación y división.
Suma de fracciones
Cómo sumar fracciones con denominador común
Sumar fracciones con el mismo denominador es muy sencillo: solo tenemos que sumar los numeradores, dejando el denominador igual. Vamos a verlo con un ejemplo:
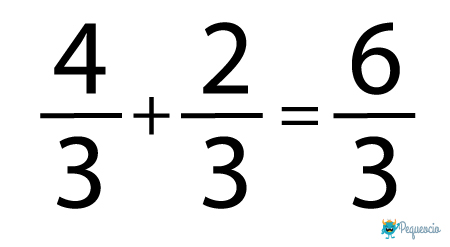
La suma de fracciones con denominador común es simple: solo se suman los numeradores, es decir los números de arriba, dejando el denominador tal cual es.
Suma de fracciones con distinto denominador
En el caso de que los denominadores sean diferentes, las operaciones con fracciones son algo más complejas. Vamos a ver un ejemplo de una suma con distinto denominador:
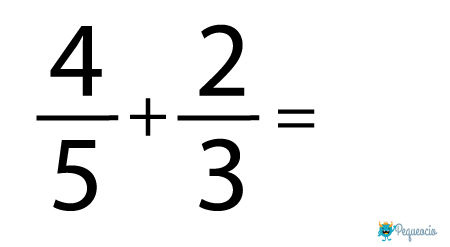
Para poder hacer la suma, tenemos que reducir las fracciones a común denominador, es decir encontrar dos fracciones equivalentes con el mismo denominador. Y para ello tenemos que encontrar el mínimo común múltiplo de los denominadores.
El mínimo común múltiplo de dos o más números es el menor número que es múltiplo común de todos ellos.

Por ejemplo: el mínimo común múltiplo de 6 y 3 es 6, porque es el primer número que coincide en los resultados de las tablas de multiplicar de ambos números.
En el vídeo está muy bien explicado, pero vamos a verlo con nuestro ejemplo: tenemos que sumar 4/5 + 2/3.
- Tenemos que reducir las fracciones a común denominador. En nuestro caso, tenemos que encontrar el m.c.m. (mínimo común múltiplo) entre 5 y 3. Repasamos las tablas del 5 y del 3, y buscamos el primer resultado que coincida entre las dos tablas, excluyendo el 0 (cero):
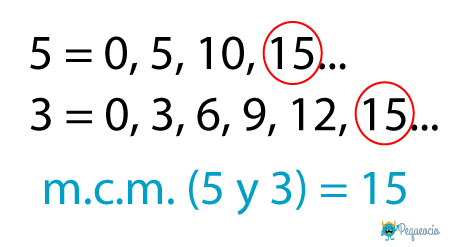
- Ya sabemos que el común denominador es 15. Ahora tenemos que dividir 15 entre cada uno de los denominadores, y el resultado multiplicarlo por el nominador de la misma fracción. De este modo obtendremos dos fracciones equivalentes con un denominador común: 15 entre 5 da 3, multiplicado por 4 da 12. La primera fracción nos queda 12/15. Hacemos lo mismo con la segunda fracción:
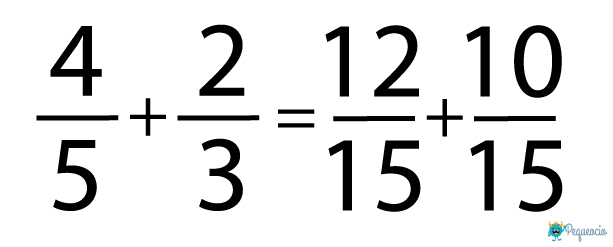
- Ahora ya podemos hacer la suma como hemos visto antes:
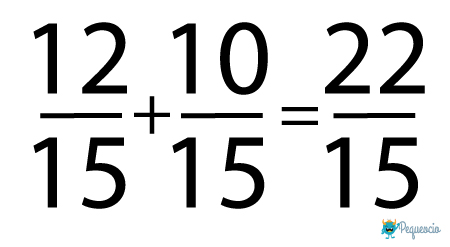
22/15 no se puede simplificar, es una fracción irreducible (es decir que no existe una fracción equivalente con números más sencillos). Por lo tanto, el resultado de 4/5 + 2/3 = 22/15
Resta de fracciones
Cómo restar fracciones con denominador común
La resta de fracciones con el mismo denominador es igual a la suma: se restan los numeradores y el denominador queda igual:
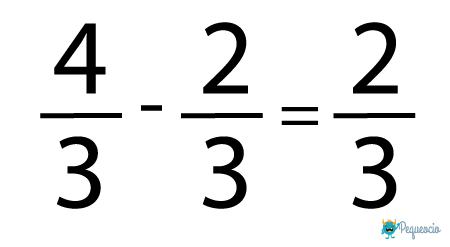
Resta de fracciones con distinto denominador
Se hace exactamente igual que la suma, por lo tanto:
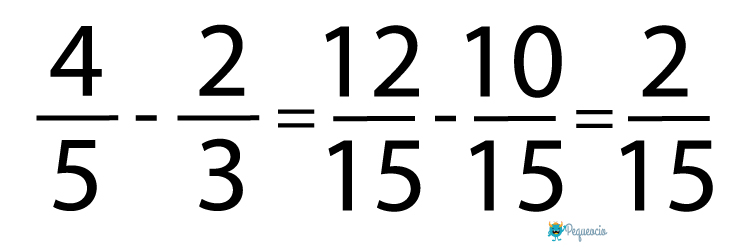
Multiplicación de fracciones
Ahora te preguntarás cómo se multiplican las fracciones; es muy fácil, porque no importa si los denominadores son iguales o diferentes. Las fracciones se multiplican en línea, es decir numerador con numerador y denominador con denominador:
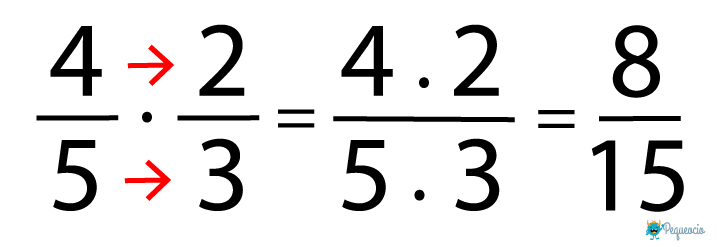
De nuevo, el resultado es una fracción irreducible, es decir que no se puede simplificar (porque el 15 es un número primo). Pero si fuera posible, siempre hay que simplificar el resultado. Por ejemplo:
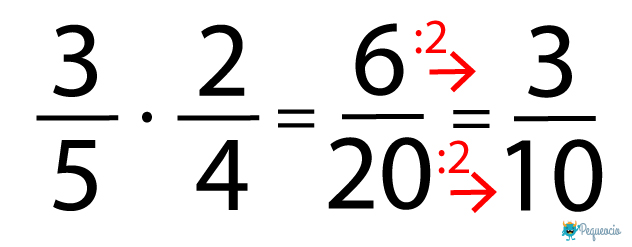
Para simplificar una fracción, divide los números de arriba y abajo por el mayor número que
divida a los dos exactamente.
Ya hemos visto cómo multiplicar fracciones, nos queda la división.
División de fracciones
Vamos a ver cómo dividir fracciones. Para dividir fracciones, tampoco es necesario que tengan denominador común. Las fracciones se dividen multiplicando en cruz:
- El numerador de la primera fracción por el denominador de la segunda = numerador final
- El denominador de la primera fracción por el numerador de la segunda = denominador final
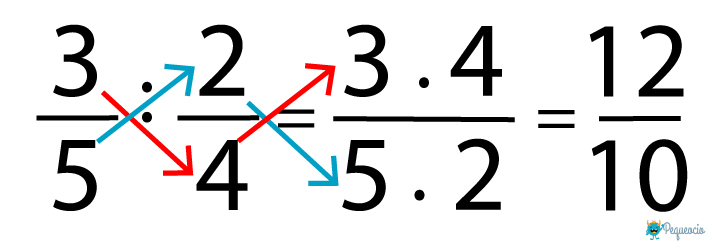
Nos acordamos siempre de simplificar el resultado, y nos queda así:
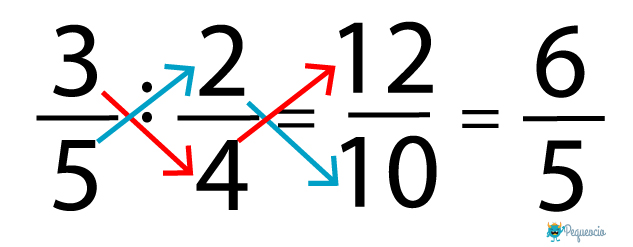
Operaciones combinadas con fracciones
Para realizar operaciones combinadas con fracciones, tenemos que recordar la jerarquía de las operaciones, es decir cuáles son las operaciones que tenemos que resolver primero:

En este vídeo está muy bien explicado. Vamos a recordarlo brevemente:
- En primer lugar se resuelven las operaciones entre paréntesis
- Luego multiplicaciones y divisiones
- Por último sumas y restas
Veamos un ejemplo de operaciones combinadas con fracciones:
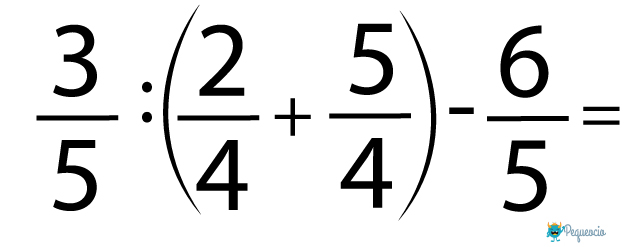
Comenzamos resolviendo la suma que está entre paréntesis, como hemos visto antes:
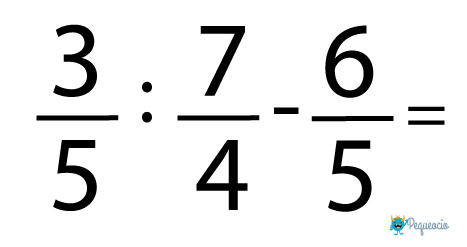
Seguimos con la división:
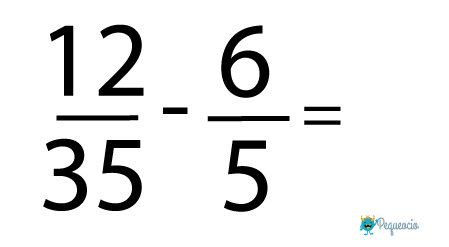
Y ya solo nos queda hacer la resta:
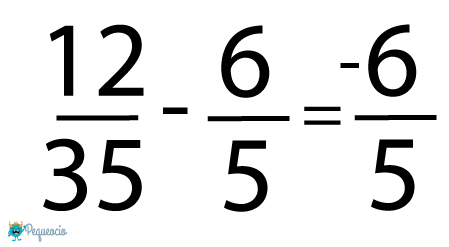
Como veis, en las fracciones puede haber números negativos, pero de eso hablaremos en otra ocasión. Ahora ¡a practicar!




