Seguimos aprendiendo geometría, esta vez es el turno del cuadrilátero, una forma básica que todos conocemos muy bien… ¿o no? Como su nombre lo indica, los cuadriláteros son formas geométricas de cuatro lados, pero van mucho más allá del simple cuadrado.
En este artículo encontrarás toda la información sobre los cuadriláteros: elementos, ángulos y tipos, explicados de manera sencilla para niños de primaria.
ÍNDICE DE CONTENIDOS
Qué es un cuadrilátero
Según la definición de la Real Academia Española:
Un cuadrilátero es un polígono que tiene cuatro lados y cuatro ángulos.
Aunque lo más correcto sería decir que es un polígono con cuatro lados (a, b, c, d) y cuatro vértices (A, B, C, D).
Elementos de un cuadrilátero
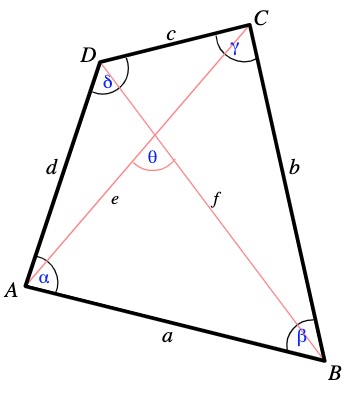
Los cuadriláteros tienen siempre las siguientes características en común:
- Tienen cuatro vértices (A,B,C,D), que son los puntos de intersección de los lados.
- Cuatro lados (a, b, c, d): son los segmentos que unen dos vértices contiguos, y forman el perímetro del cuadrilátero.
- Tienen dos diagonales (e, f), que son los segmentos cuyos extremos son dos vértices no contiguos.
- Cuatro ángulos interiores (?, ?, ?, ?), determinados por dos lados contiguos.
- Cuatro ángulos exteriores, determinados por la prolongación exterior de un lado y su lado contiguo.
- Un incentro, que es el centro de la circunferencia inscrita en el cuadrilátero.
Tipos de cuadriláteros
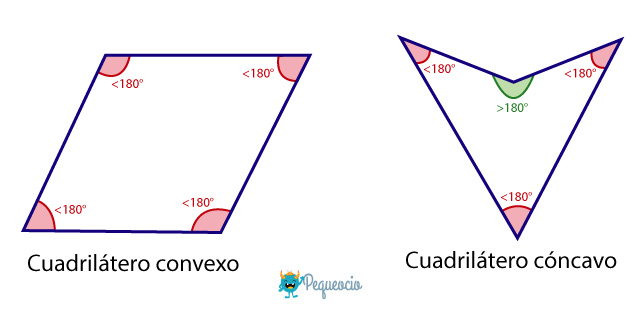
Los cuadriláteros se clasifican en dos clases según sus ángulos interiores:
- Convexos: todos sus ángulos interiores son menores de 180º. La suma de sus ángulos interiores es de 360º y sus dos diagonales son interiores.
- Cóncavos: al menos uno de sus ángulos interiores mide más de 180º. Al menos una de sus dos diagonales es exterior.
Los cuadriláteros convexos se pueden dividir en varias categorías según sus lados y ángulos:
Paralelogramos
Los paralelogramos son cuadriláteros con los lados opuestos paralelos.
Se clasifican en:
Cuadrado
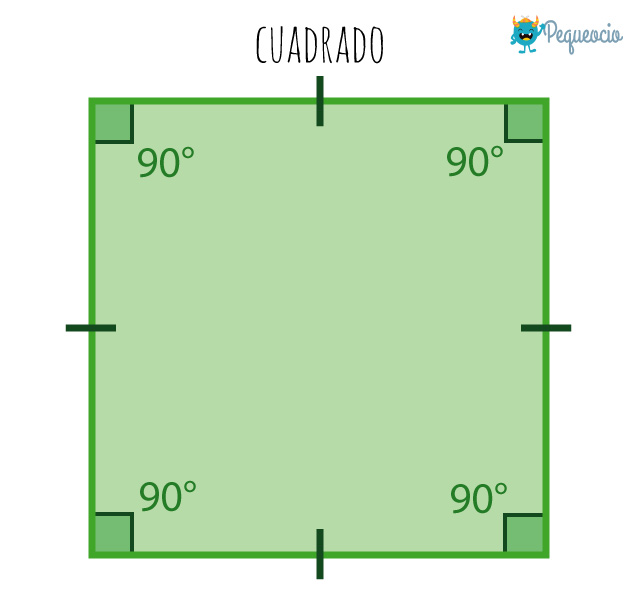
Un cuadrado tiene los cuatro lados iguales, sus cuatro ángulos interiores rectos, sus diagonales son iguales y perpendiculares entre sí, tiene una circunferencia inscrita (la circunferencia más grande contenida en el polígono) y otra circunscrita (que pasa por todos los vértices de un polígono y contiene completamente a dicha figura en su interior).
Rectángulo
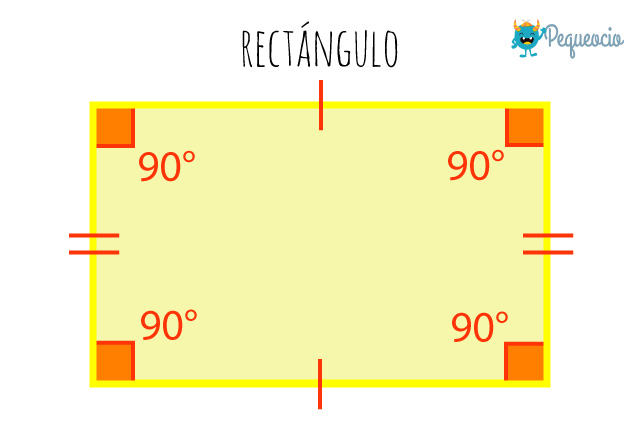
Un rectángulo tiene los lados opuestos iguales, y diferentes a los contiguos. Sus cuatro ángulos interiores son rectos, sus dos diagonales son iguales pero no son perpendiculares entre sí y tiene una circunferencia circunscrita.
Ver cómo calcular el perímetro de un rectángulo
Rombo
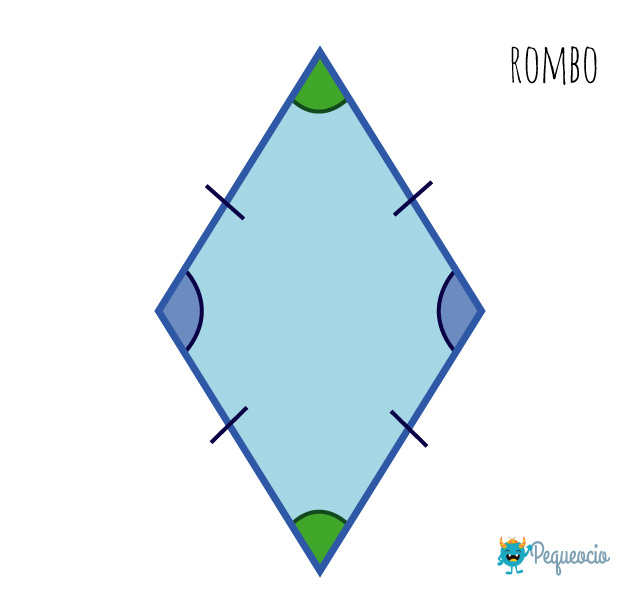
El rombo tiene los cuatro lados iguales, y los ángulos opuestos iguales, pero diferentes de los contiguos (dos obtusos y dos agudos). Sus diagonales son distintas y perpendiculares entre sí, y tiene una circunferencia inscrita.
Mira cómo se calcula el área de un rombo
Romboide
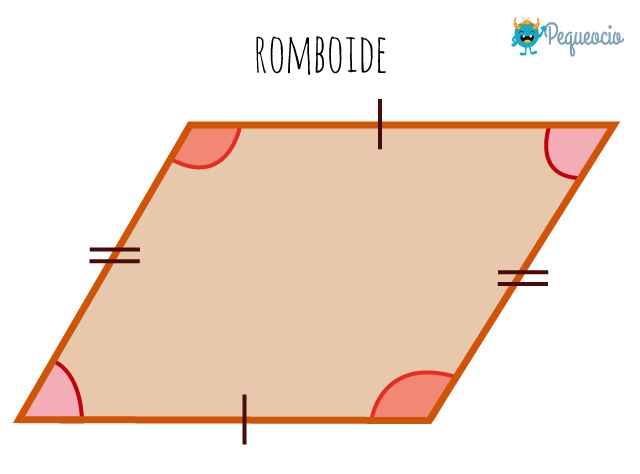
Sus lados opuestos son iguales, pero diferentes a los contiguos. Tiene los ángulos opuestos iguales, pero diferentes de los contiguos (dos obtusos y dos agudos). sus dos diagonales son de distinta longitud y no son perpendiculares entre sí.
Área del paralelogramo
En la forma más sencilla para calcular el área de un paralelogramo necesitamos conocer la medida de la base relativa a uno de sus lados. Tomamos un lado cualquiera como base (b), y la altura de dicho lado (h), y los multiplicamos.
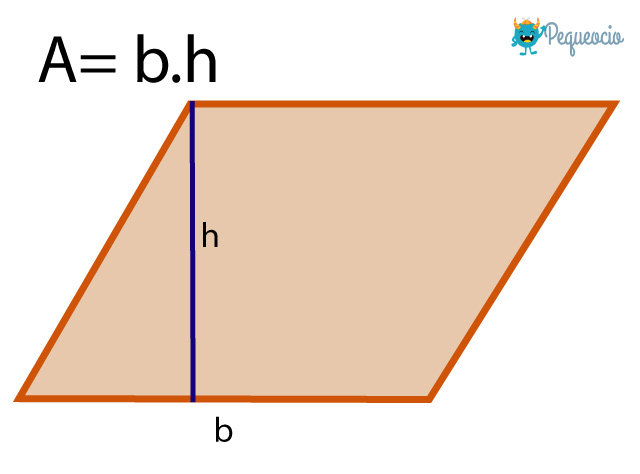
La fórmula para calcular el área de un paralelogramo es A = b.h
Perímetro del paralelogramo
Como el paralelogramo tiene los lados iguales de a dos, el perímetro será la suma de dos lados diferentes multiplicada por 2:
P = 2 . (a + b)
Siendo a y b los lados diferentes.
Nos queda mencionar a los cuadriláteros que no son paralelogramos:
Trapecio
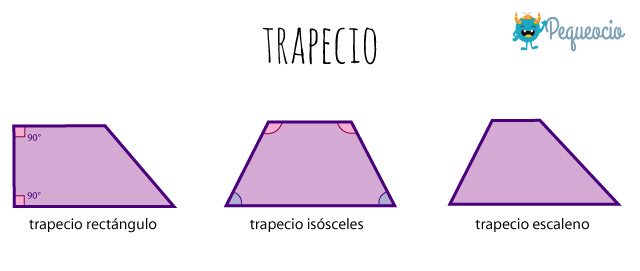
El trapecio tiene dos lados opuestos paralelos, de diferente longitud. Los lados paralelos se llaman base del trapecio, y los no paralelos altura del trapecio.
Se pueden clasificar en:
- rectángulo: cuando tiene dos ángulos interiores consecutivos rectos.
- isósceles: tiene los lados no paralelos de la misma medida, dos ángulos interiores agudos iguales en una base y dos ángulos interiores obtusos iguales en la otra base.
- escaleno: sus cuatro ángulos interiores son diferentes.
Área de un trapecio
Para calcular el área del trapecio necesitamos conocer su altura y la longitud de sus lados paralelos, es decir de sus bases. Debemos multiplicar la altura (h) por la mediana del trapecio (M), que es la media de las dos bases a y b: M= (a+b)/2
La fórmula para calcular el área del trapecio es:
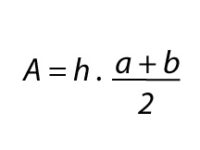
Existen otras fórmulas, pero esta es la más sencilla.
Perímetro de un trapecio
El trapecio puede tener sus cuatro lados desiguales, por lo que su perímetro (P) es la suma de los cuatro lados:
P = a + b + c + d
En el caso del trapecio isósceles, que tiene dos lados no paralelos (c) de la misma medida, la fórmula sería:
P = a + b + c.2
Trapezoide
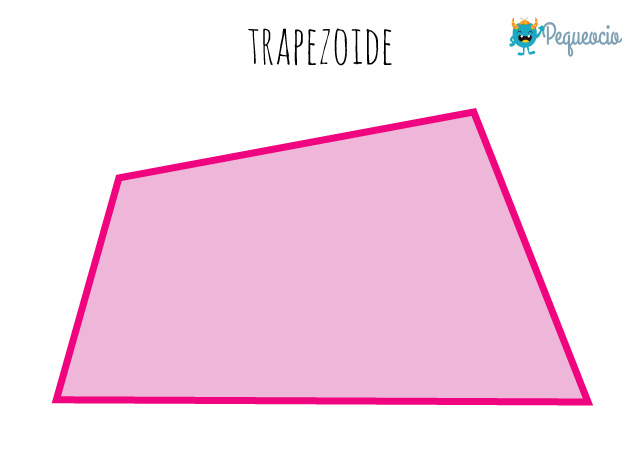
Cuando un cuadrilátero no tiene ningún lado paralelo, se llama trapezoide.
Área del trapezoide
Para calcular el área del trapezoide debemos dividirlo en dos triángulos, calcular el área de cada uno y luego sumar los resultados.
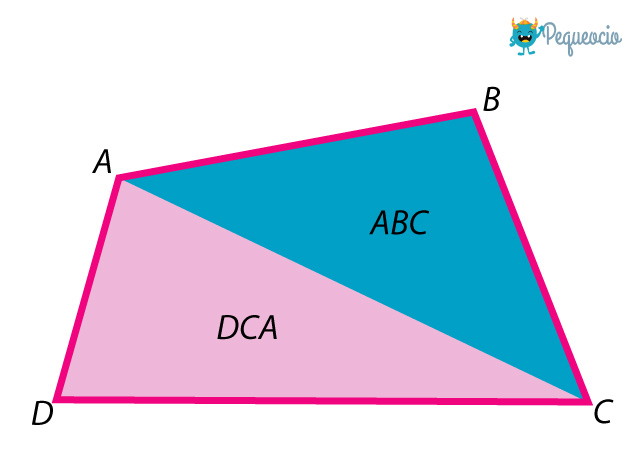
Tenemos entonces los triángulos ABC y DCA. La base de ambos triángulos es el segmento AC.
? Recuerda que el área de un triángulo se calcula multiplicando base por altura dividido entre dos:
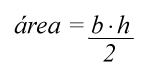
Por lo tanto, la fórmula para calcular el área del trapezoide es:
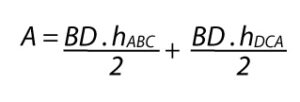
Siendo BD la base de los triángulos, y h sus alturas.
Existen otros modos, más complejos, por ahora nos quedamos con este.
Perímetro del trapezoide
El trapezoide puede tener sus cuatro lados desiguales, por lo que su perímetro (P) es la suma de los cuatro lados:
P = a + b + c + d
En el caso del trapezoide deltoide (como una cometa), que tiene los lados iguales de a dos la fórmula sería:
P = 2. (a + b)
Hasta aquí llegamos con nuestra lección básica sobre cuadriláteros. Sigue aprendiendo geometría con nosotros:

