Vamos a aprender a calcular el área del trapecio: un trapecio es un cuadrilátero, es decir una figura de 4 lados, pero ya veremos su definición más adelante.
Hay varias formas de sacar el área de un trapecio, pero en esta ocasión os vamos a explicar la más sencilla, a partir de sus bases y su altura, ya que es una explicación para primaria. Vamos a verlo.
¿Qué es un trapecio?
El trapecio es una figura geométrica de 4 lados, que tiene dos lados opuestos paralelos, de diferente longitud.
Los lados paralelos se llaman base del trapecio la más larga es la mayor y la otra la menor; y los no paralelos altura del trapecio.
Se pueden clasificar en:
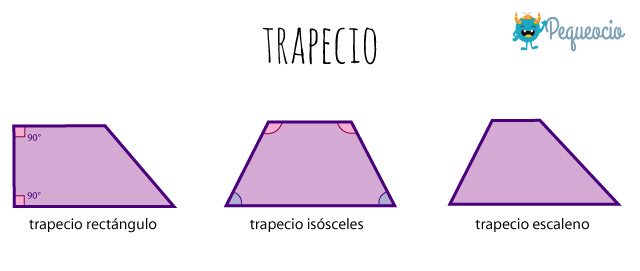
- rectángulo: cuando tiene dos ángulos interiores consecutivos rectos.
- isósceles: tiene los lados no paralelos de la misma medida, dos ángulos interiores agudos iguales en una base y dos ángulos interiores obtusos iguales en la otra base.
- escaleno: sus cuatro ángulos interiores son diferentes.
Cómo se calcula el área de un trapecio
Recordemos antes de empezar que el área es la superficie comprendida dentro de un perímetro, que se expresa en unidades de medidas que son conocidas como superficiales (cm2, m2, etc.)
Hemos dicho ya que existen diferentes fórmulas para calcular el área del trapecio. Vamos a explicar la más sencilla.
Para calcular el área de un trapecio necesitamos conocer su altura (h) y la longitud de sus lados paralelos, es decir de sus bases (a y b).
RECUERDA ? La altura de un trapecio es la distancia entre las dos bases.
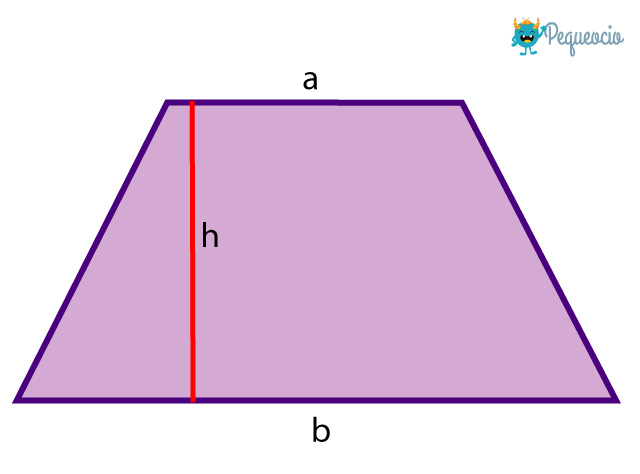
Debemos multiplicar la altura (h) por la mediana del trapecio (M), que es la media de las dos bases a y b: M= (a+b)/2
La fórmula para calcular el área del trapecio es:
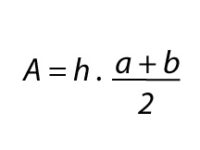
Vamos a verlo con un ejemplo: tenemos el siguiente trapecio:
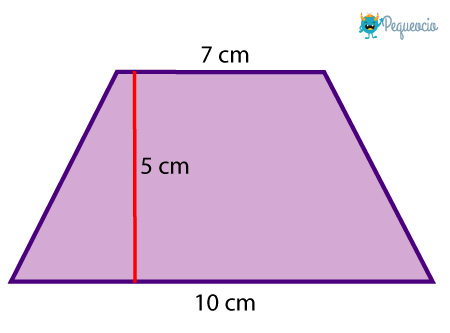
Vamos a reemplazar los datos que tenemos en la fórmula:
A = 5cm . (7cm + 10cm) : 2
A = 5cm . 17cm : 2
A = 85cm2 : 2
A = 42,5 cm2
El trapecio tiene un área de 42,5 cm2
Como veis es muy sencillo, existen otras fórmulas para calcular el área a partir de la medida de sus lados, haciendo una operación geométrica a partir de la fórmula de Herón, o a partir de las longitudes de sus diagonales y el ángulo que forman al cruzarse, pero son todas demasiado complejas para el nivel de primaria. Así que nos quedaremos con esta explicación sencilla ¿qué os parece?
No olvidéis que en Pequeocio encontraréis mucho más material didáctico de Geometría, aquí os dejamos algunos ejemplos:

