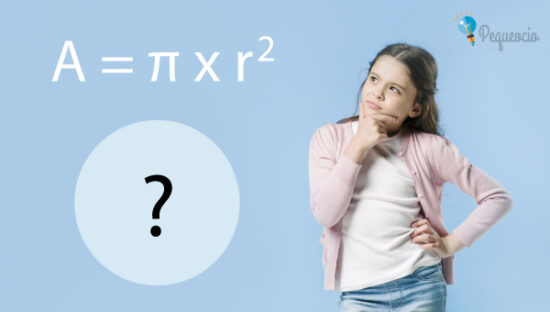Calcular el área del círculo es un ejercicio por el que todos pasamos durante nuestra vida escolar… y es probable que apliquemos una fórmula, sin entender de todo qué significa. Pero entender es la clave para aprender de verdad, es decir para que eso que hemos aprendido no se nos olvide después de poco tiempo.
Así que en esta ocasión vamos a explicar de forma FÁCIL qué es el área de un círculo y cómo se calcula. Para ello vamos a repasar los elementos del círculo que tenemos que conocer para poder calcular su área: la circunferencia, el radio, el diámetro… ¿y el número PI? ¿Sabéis qué representa?
No os preocupéis porque con nuestra explicación, el área del círculo va a ser pan comido para vosotros.
ÍNDICE DE CONTENIDOS
¿Qué es el área del círculo?
Pero para poder entender cómo se calcula el área del círculo, primero tenemos que conocer los elementos que lo componen:
Elementos del círculo
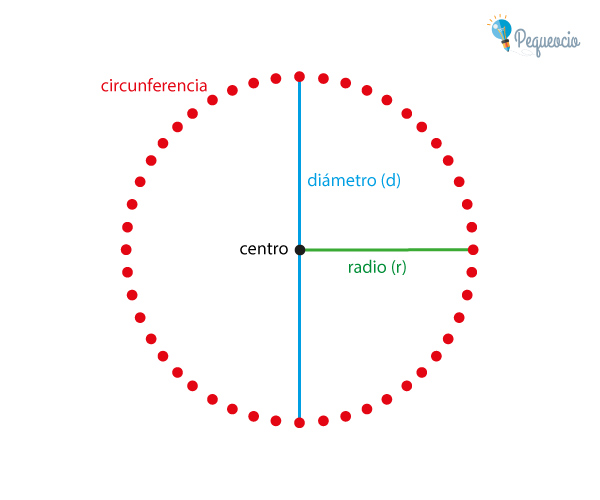
Circunferencia
La circunferencia de un círculo es su contorno, su límite. En términos matemáticos, la circunferencia es una curva plana y cerrada, formada por un conjunto de puntos que se encuentran a igual distancia de otro llamado centro.
Se suele confundir términos, usando círculo y circunferencia como sinónimos, cuando no lo son: como hemos dicho la circunferencia es la línea que delimita al círculo, que posee un área definida… pero de eso nos ocuparemos más adelante.
Radio
El segmento que une el centro del círculo con cualquier punto de la circunferencia, se llama radio.
Diámetro
El segmento que une dos puntos de la circunferencia, pasando por el centro, se llama diámetro.
El número PI, relación entre la longitud de la circunferencia y su diámetro
El famoso número PI, cuyo símbolo es π, es la relación entre la longitud de una circunferencia y su diámetro. Es decir, las veces que el diámetro entra en la circunferencia. Es un número constante, porque no importa cuál sea la circunferencia del círculo, el número π será siempre el mismo. Tiene un número indefinido de decimales (actualmente se han calculado dos billones y medio), pero para realizar cálculos matemáticos se utilizan cuatro:
π = 3.1416
Perímetro de la circunferencia
El perímetro de la circunferencia es la medida de su longitud. Supongamos que la circunferencia de nuestro círculo es un hilo, y que podemos extenderlo: la longitud de este hilo es el perímetro de la circunferencia. Pero ¿cómo se calcula? Tenemos dos fórmulas posibles:
- Multiplicando PI (π) por el diámetro (d): P =π x d
- Multiplicando dos veces PI (π) por el radio (r): P = 2π x r
Recordemos que el número π es 3.1416
Veamos un ejemplo: si tenemos un círculo de 5 cm de diámetro, y por lo tanto de 2,5 cm de radio, el resultado es el siguiente usando la primera fórmula:
P =π x d
P = 3.1416 x 5
P = 15,708 cm
Si usamos la segunda fórmula:
P = 2π x r
P = 2(3.1416) x 2.5
P = 6.2832 x 2.5
P = 15,708 cm
Aprende más sobre el perímetro
¿Cómo se calcula el área del círculo?
Ahora conocemos todos los elementos necesarios para calcular el área del círculo. Existe una fórmula precisa, que es la siguiente:
A = π x r²
Por lo tanto, para calcular el área de un círculo, debemos conocer su radio (r) o su diámetro, ya que es el doble del radio. Aplicando esta fórmula podemos calcular el área, pero no hemos entendido por qué se calcula así ¿verdad? vamos a seguir aprendiendo.
Fórmula para calcular el área de un círculo
Para explicar el origen de la fórmula para calcular el área de un círculo, vamos a hacerlo con un ejemplo:
Tenemos un círculo de 2.5 cm de radio (r), con un perímetro de la circunferencia (p) de 15.708 cm. Vamos a dividir este círculo en porciones iguales, como si cortáramos una pizza:
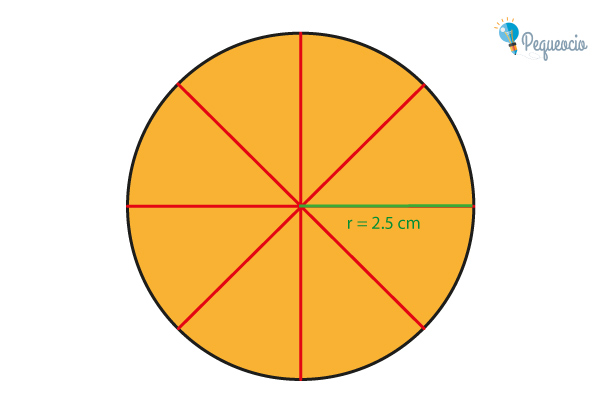
Ahora vamos a colocar esas porciones de círculo una al lado de la otra; si las encerramos en un rectángulo, este rectángulo tendrá 15.708 cm de base (el perímetro de la circunferencia), por 2.5 cm de alto (el radio):
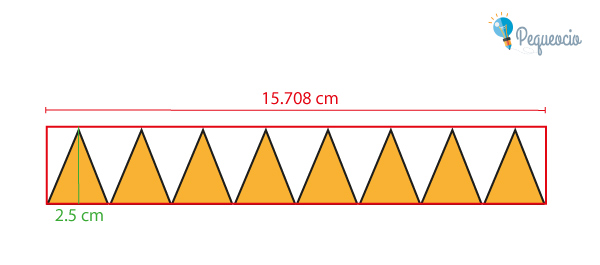
Ahora, para calcular el área, tenemos que hacer perímetro (p) x radio(r) dividido por 2: multiplicando p x r obtenemos el área del rectángulo en el que hemos englobado nuestras «porciones» de círculo; pero el área ocupada por las porciones, es decir el área del círculo, es la mitad del área del rectángulo, por eso lo dividimos por 2:
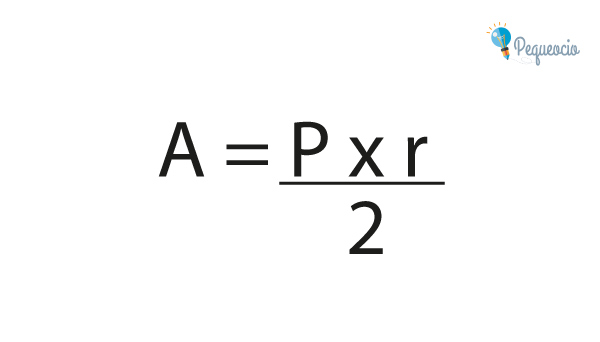
Si reemplazamos con los datos que conocemos, vemos que el área es:
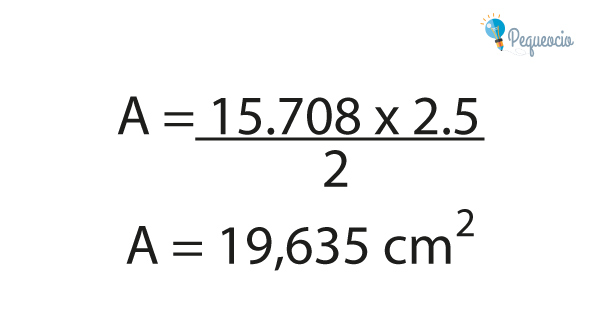
Pero para calcular el área de este modo, primero tendríamos que calcular el perímetro de la circunferencia. Por eso, vamos a seguir simplificando la fórmula. Vamos a reemplazar «p», por la fórmula que hemos usado para calcularlo:
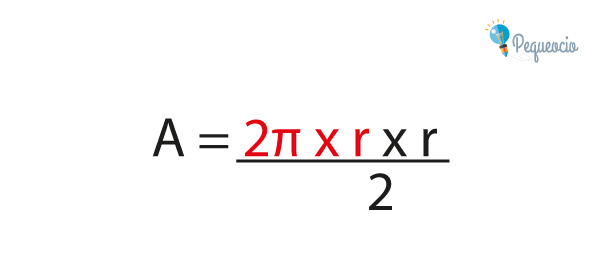
Como tenemos un 2 que multiplica y otro que divide, podemos eliminarlos:
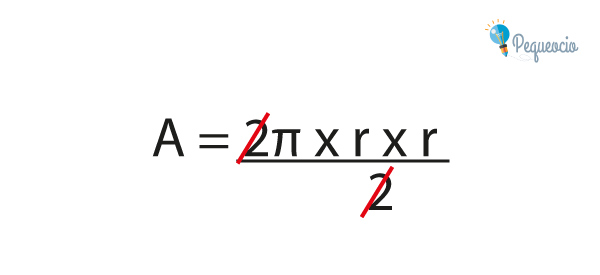
Nos queda entonces la fórmula A = π x (r x r)
r x r es igual que r al cuadrado (r²), así que finalmente, la fórmula para calcular el área del círculo es:
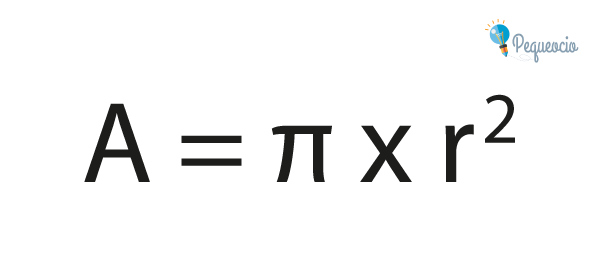
Vamos a comprobar nuestro primer calculo reemplazando con los datos que tenemos:
A = 3,1416 x 2.5²
A= 3.1416 x 6,25
A = 19.635 cm²
Hemos llegado al mismo resultado.
Otras fórmulas para calcular el área de un círculo
Peo el área se puede calcular también a partir del diámetro (d):
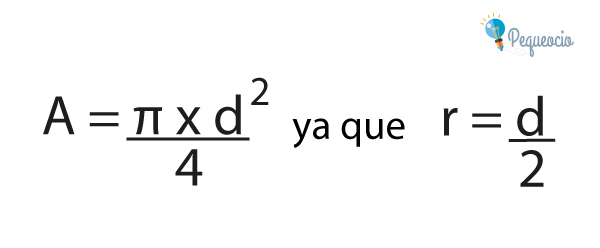
O a partir del perímetro de la circunferencia (p):
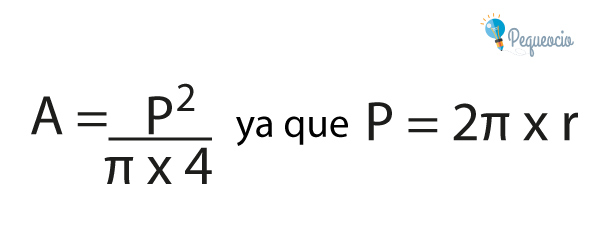
Si haces la prueba reemplazando los términos por los datos que tienes, verás que siempre llegas al mismo resultado.
Ejercicios para calcular el área del círculo
A esta altura, ya tienes clarísimo cómo se calcula el área del círculo. Vamos a ponerte a la prueba con estos ejercicios:
Ejercicio 1
Calcula el área de un círculo de 4 cm de radio: r = 4 cm
Ejercicio 2
Calcula el área de un círculo de 7 cm de diámetro: d = 7 cm
Ejercicio 3
Calcula el área de un círculo de 35 cm de perímetro: p = 35 cm
¿Cómo te fue con estos ejercicios para calcular el área de un círculo…?
Pues si quieres saber más sobre cómo calcular diferentes formas geométricas, a continuación te dejamos cómo calcular el área de un rectángulo, el área de un cuadrado, el área del trapecio, el área de un triángulo y finalmente cómo calcular el área de un rombo.
Necesito ayuda para resolver este ejercicio.
¿que distancia recorre un coche al dar una vuelta a una rotonda de 230 metros de ancho y que superficie necesitamos asfaltar si queremos cubrirla de cemento?