La suma de fracciones es una de las operaciones con fracciones más sencillas, de hecho la primera que se aprende. Si estás en ello en el cole, o si necesitas repasar durante las vacaciones, estás en el lugar indicado: vamos a explicar de la manera más fácil cómo sumar fracciones, ya sea con denominador común que con distinto denominador.
Después de que nos haya quedado muy clarita la explicación, vamos a ver ejercicios con fracciones para practicar, y también te dejaremos los resultados para que compruebes si los has resuelto bien.
ÍNDICE DE CONTENIDOS
Cómo sumar fracciones con denominador común
La suma de fracciones con el mismo denominador es realmente muy sencilla: solo se suman los numeradores, es decir el número de arriba. El denominador queda igual, no tenemos que hacer ninguna operación con él.
Mira este ejemplo:
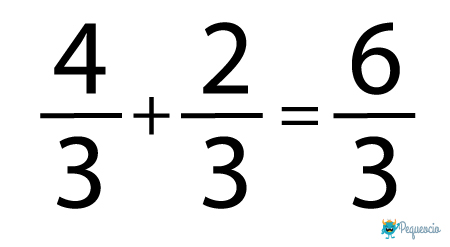
Como ves, solo sumamos los numeradores, es decir 4+2, y mantenemos el denominador tal cual es. No importa cuántas fracciones estés sumando, si el denominador es el mismo, siempre tendrás que dejarlo tal cual y solo sumar los numeradores.
Suma de fracciones con distinto denominador
La operación se complica cuando se trata de sumar fracciones con distinto denominador. En este caso necesitamos reducir las fracciones a común denominador, es decir encontrar dos fracciones equivalentes a las que tenemos que sumar, que tengan el mismo denominador. ¿No recuerdas qué son las fracciones equivalentes? Ahora mismo te lo explicamos.
Fracciones equivalentes
Las fracciones equivalentes (iguales) son aquellas fracciones que representan la misma cantidad.
Te quedará muy claro con esta imagen:
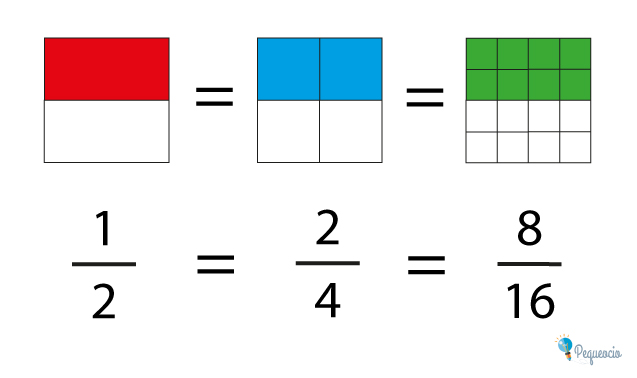
Estos tres cuadrados son iguales, pero están divididos en diferentes cantidades de partes. El primero está dividido en 2 partes, el segundo en 4 y el tercero en 16. En cada uno de los cuadrados, hemos tomado algunas partes (las hemos coloreado para que lo entiendas): en el primer cuadrado tomamos 1 parte de 2, por lo tanto la fracción es 1/2. En el segundo tomamos 2 partes de 4 totales, y la fracción es 2/4; en el tercer cuadrado hemos tomado 8/16. Si te fijas bien, las partes coloreadas, es decir las que representan las partes que hemos cogido (el numerador de las fracciones) son iguales; esto significa que aunque las fracciones son diferentes, representan la misma cantidad de partes tomadas de un todo, y por lo tanto son equivalentes.
¿Te ha quedado claro? Si te queda alguna duda te lo explicamos mejor aquí> FRACCIONES EQUIVALENTES
Ahora bien, para poder encontrar las fracciones equivalentes a las nuestras con el mismo denominador para poder hacer la suma, tenemos que encontrar el mínimo común múltiplo de los denominadores… ¿y qué es esto?
Mínimo común múltiplo
Vamos a verlo con un ejemplo. Digamos que queremos sumar estas fracciones:
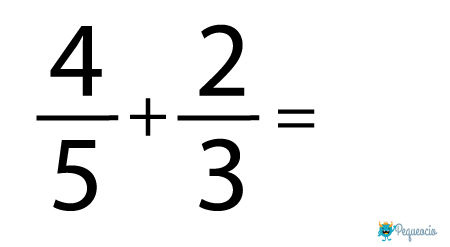
Necesitamos calcular el mínimo común múltiplo de los denominadores, es decir de 5 y 3.
El mínimo común múltiplo de dos o más números es el menor número que es múltiplo común de todos ellos.
Por ejemplo: el mínimo común múltiplo de 6 y 3 es 6, porque es el primer número que coincide en los resultados de las tablas de multiplicar de ambos números.
En el vídeo está muy bien explicado, pero vamos a verlo con nuestro ejemplo: tenemos que sumar 4/5 + 2/3.
- Tenemos que reducir las fracciones a común denominador. En nuestro caso, tenemos que encontrar el m.c.m. (mínimo común múltiplo) entre 5 y 3. Repasamos las tablas del 5 y del 3, y buscamos el primer resultado que coincida entre las dos tablas, excluyendo el 0 (cero):
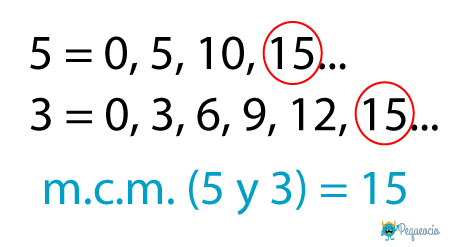
- Ya sabemos que el común denominador es 15. Ahora tenemos que dividir 15 entre cada uno de los denominadores, y el resultado multiplicarlo por el nominador de la misma fracción. De este modo obtendremos dos fracciones equivalentes con un denominador común: 15 entre 5 da 3, multiplicado por 4 da 12. La primera fracción nos queda 12/15. Hacemos lo mismo con la segunda fracción:
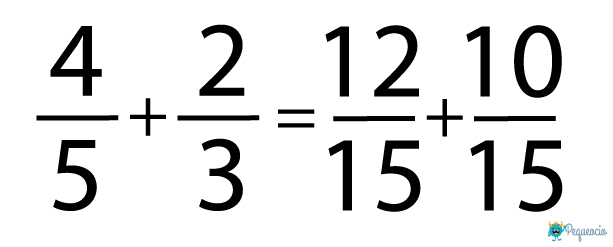
- Ahora ya podemos hacer la suma como hemos visto antes:
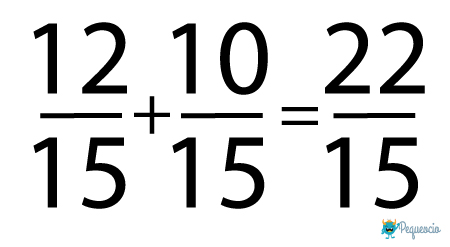
22/15 no se puede simplificar, es una fracción irreducible (es decir que no existe una fracción equivalente con números más sencillos). Por lo tanto, el resultado de 4/5 + 2/3 = 22/15
Suma de fracciones con el método de los productos cruzados
Hay otro método para sumar fracciones que consiste en multiplicar. Vamos a resolver la misma operación con este otro método:
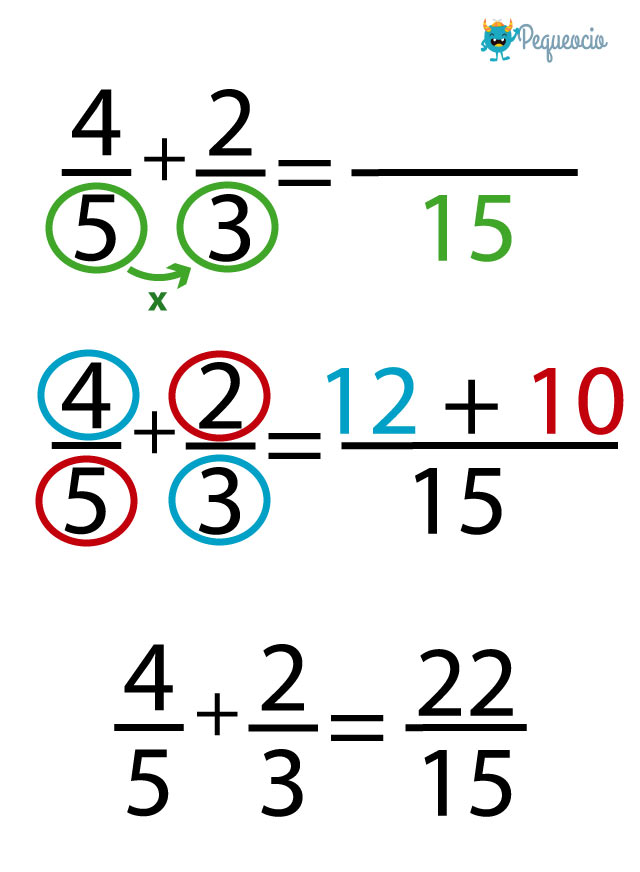
- Multiplicamos los denominadores: 5×3 nos da 15. Lo escribimos en el denominador del resultado.
- Ahora multiplicamos el denominador de cada fracción por el numerador de la otra fracción: multiplicamos 4 (el numerador de la primera fracción) x 3 (el denominador de la segunda fracción), y nos da 12. Repetimos con 5×2, que nos da 10. Sumamos estos dos productos cruzados, 12+10, y el resultado (22) lo ponemos en el numerador.
En este caso hemos obtenido el mismo resultado que con el método del m.c.m., pero no siempre es así, porque puede que haya un m.c.m. que sea menor al resultado de la multiplicación de los dos denominadores. Vamos a ver un ejemplo:
3/6 + 1/2
Con el método del m.c.m. lo resolvemos así:
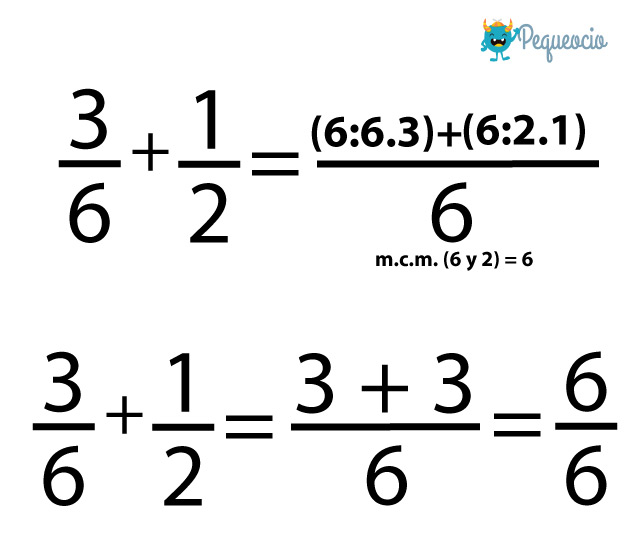
El resultado de 3/6 + 1/2 es 6/6
Si lo resolvemos con el método de los productos cruzados, será así:
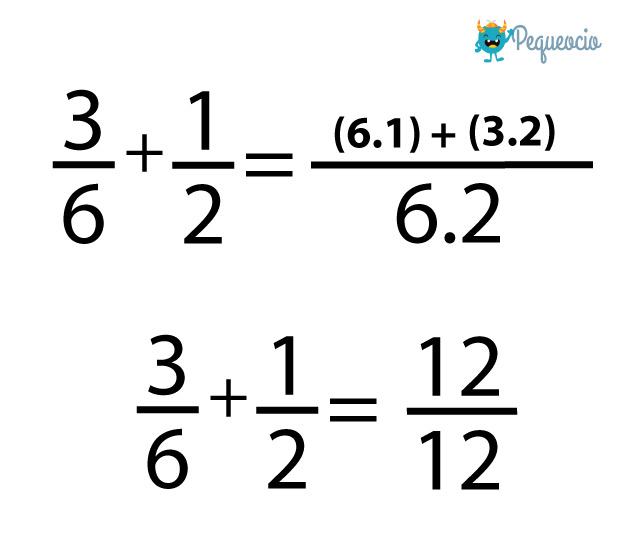
En este caso el resultado es 12/12. Pero 6/6 y 12/12 son fracciones equivalentes, por lo tanto el resultado es correcto en ambos casos.
Recuerda que siempre tienes que simplificar el resultado hasta llegar a una fracción irreducible: una fracción no se puede reducir más cuando sus términos no tienen ningún divisor común excepto el 1.
Ejercicios de sumas de fracciones
Resuelve las siguientes sumas de fracciones:
- 2/3 + 5/6
- 30/15 + 15/9
- 30/20 + 15/9
- 7/15 + 11/35
- 40/25 + 49/28
- 32/16 + 40/100 + 12/20
- 2/9 + 7/12 + 32/34
- 40/80 + 23/69 + 17/102









excelentes ejercicios, me encantaron, pude entender a la perfección con estos ejemplos.
gracias.
Gracias, despues de lidiar tanto con este tema por fin lo comprendo, para explicarlo a mis peques.