Si en el cole ya estáis aprendiendo las fracciones, seguro que las fracciones equivalentes son uno de las primeras cosas que aprenderéis. Hoy os vamos a explicar qué son, y también cómo saber cuándo una fracción es equivalente a otra.
Os lo vamos a explicar de manera muy sencilla, con la ayuda de gráficos para que lo entendáis aún mejor. Y para terminar, os vamos a dejar ejercicios de fracciones equivalentes para que practiquéis.
Antes de empezar tal vez te convenga repasar la primera lección: ¿Qué son las fracciones?
ÍNDICE DE CONTENIDOS
¿Qué son las fracciones equivalentes?
Las fracciones equivalentes (iguales) son aquellas fracciones que representan la misma cantidad.
Vamos a entenderlo mejor con la siguiente imagen:
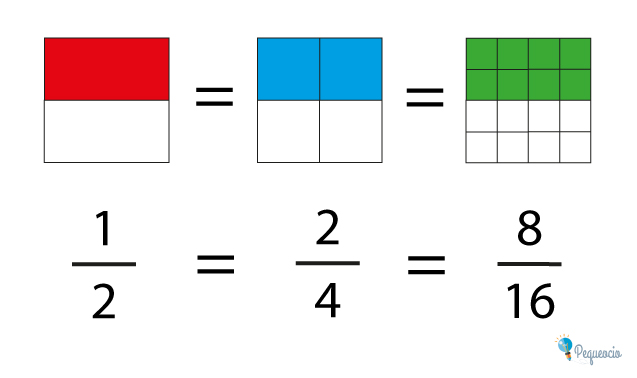
El primer cuadrado está dividido en dos partes, y hemos tomado una de ellas; si lo representamos con números su fracción será 1/2. El segundo cuadrado está dividido en cuatro partes, y hemos cogido 2; la fracción será 2/4. El último cuadrado está dividido en dieciséis partes, de las que hemos tomado 8; su fracción es 8/16.
Como puedes ver, la parte coloreada en los tres cuadrados, que representan las partes que hemos cogido (el numerador) es igual en los tres casos, aunque las fracciones son diferentes. A esto se le llama fracción equivalente.
Cómo saber si 2 fracciones son equivalentes
Hay varias maneras de saber cuando nos encontramos frente a fracciones que son equivalentes. Vamos a verlo.
Método 1: Producto cruzado
En este método debemos multiplicar el numerador de una fracción por el denominador de la otra, y comparar los resultados.
Como ejemplo, comparemos 1/2 y 2/4:
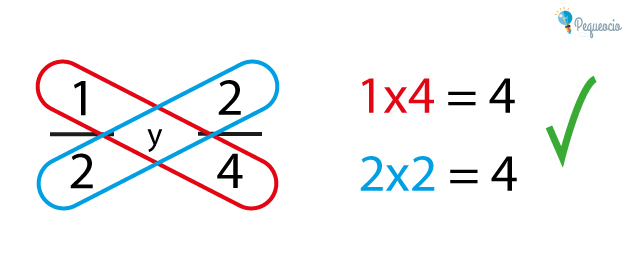
- 1×4=4
- 2×2=4
Como el resultado es el mismo, podemos decir que 1/2 y 2/4 son equivalentes.
Método 2: Dividiendo
Otro método es pasar la fracción a número decimal. Si el resultado es el mismo, las fracciones son equivalentes. Para hacerlo solo tenemos que dividir el numerador por el denominador:
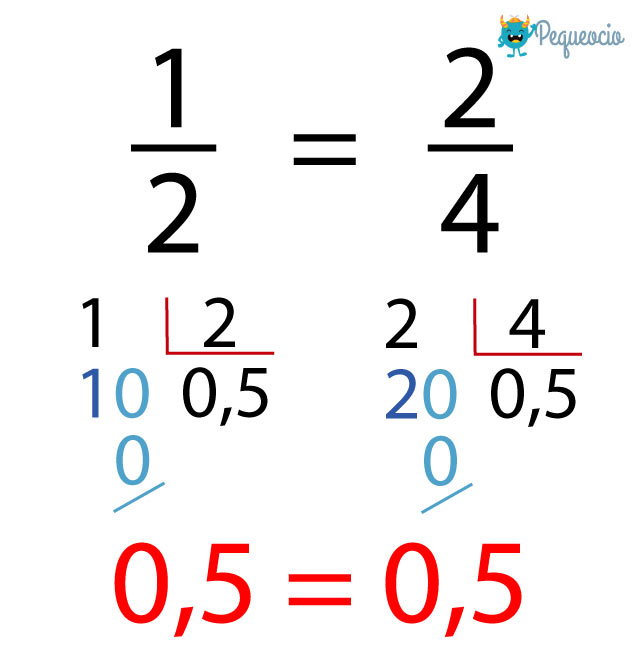
Método 3: Simplificando
Si son equivalentes, al reducirlas al máximo, es decir al llegar a una fracción irreducible (que no se puede simplificar en números más pequeños), llegaremos a la misma fracción. Para simplificar una fracción, divide el numerador y el denominador por el mayor número que divida a los dos exactamente. Vamos a verlo con un ejemplo, veamos si las fracciones 10/30 y 14/42 son equivalentes:
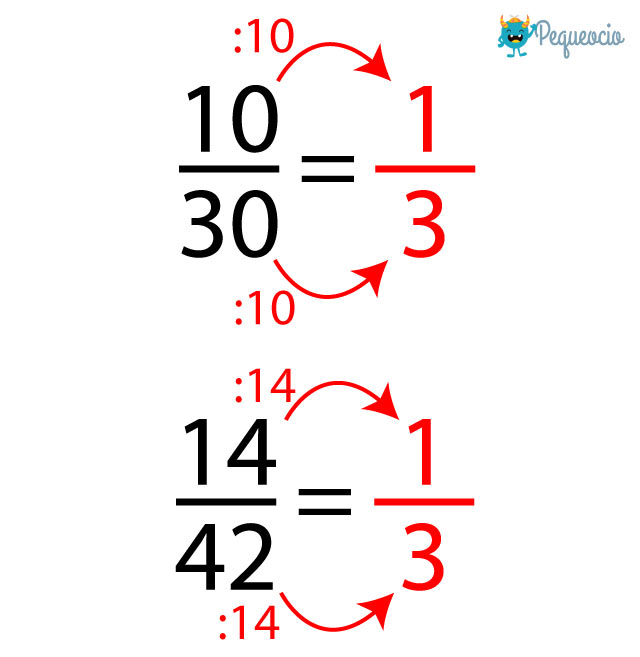
Cómo calcular fracciones equivalentes
Hasta ahora hemos visto cómo saber si dos o más fracciones son equivalentes. Pero ¿qué pasa si lo que queremos es encontrar una fracción equivalente de una fracción dada? Es muy sencillo, hay dos modos:
Por amplificación
Simplemente multiplicamos el numerador y el denominador por el mismo número, un número cualquiera. Por ejemplo, si partimos de la fracción 1/3 y la multiplicamos varias veces por 2, obtendremos varias fracciones equivalentes:
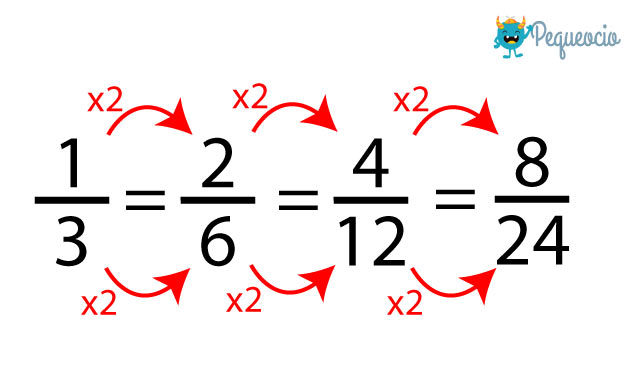
Por simplificación
En este caso dividiremos el numerador y el denominador por el mismo divisor común:
Este método no se puede utilizar siempre, porque para poder usarlo el numerador y el denominador deben tener un divisor común. Si ambos son números pares no tendréis problemas, podéis dividirlos por 2; pero en el caso de que al menos uno de los números sea impar, no siempre será posible.
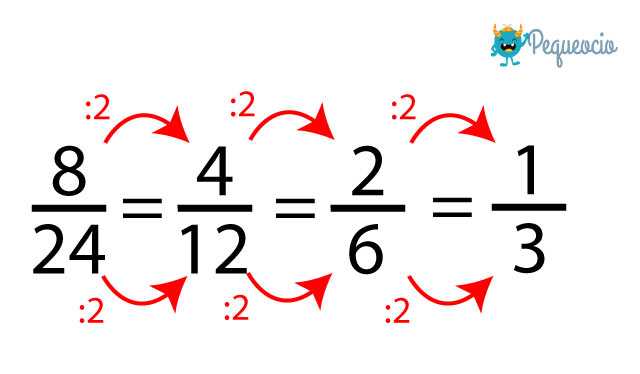
Ejercicios con fracciones equivalentes
Vamos a repasar todo lo aprendido con algunos ejercicios:
1- Indica si las siguientes parejas de fracciones son o no equivalentes
- 1/6 – 2/12
- 7/8 – 5/4
- 2/5 – 4/10
- 4/5 – 8/10
- 7/14 – 1/2
- 6/10 – 90/150
- 12/28 – 24/56
2- Completa la fracción reemplazando la X por el número correcto para que se cumpla la igualdad
- 3/4 = X/12
- X/4 = 4/12
- 2/5 = 12/X
- 2/7 = X/14
- X/2 = 8/16
- 1/X = 2/6
- 3/4 = X/16
- 1/2 = 7/X
- X/2 = 4/8
- 1/X = 6/42
Imagen principal www.freepik.com